ちりつもFILE (β 「実際どうなの？」をちりつもするブログメディア。ただいまβ運用中。
解が無数にある常微分方程式 単純な常微分方程式についても, 解の一意性は必ずしも成り立たないことを本記事では紹介します: 次の常微分方程式の初期値問題を考えましょう \begin{align*} \begin{cases} \dfrac{dx}{dt}(t) = -2\sqrt{|x(t)|},\\ x(0) = 1. \end{cases} \end{align*} まずは, これを変数分離法を […]
前川 淳: 本格折り紙―入門から上級まで. 日貿出版社, 2007/7/1 BACKGROUND ――対象 「普段は科学系の本を中心に紹介しているのに、今回は急に子供向け？」 いえいえ、そんな事はありません。 確かにこれは折り紙の本ですし、子どもでも作れるような作品も紹介されています。 しかし、本書の真骨頂は「数学の分かる大人」にこそ面白く感じられるはずで […]
古川 武彦, 大木 勇人: 図解 気象学入門 ブルーバックス, 2011/3/23 BACKGROUND ――対象 著者の古川氏は気象庁で予報を行っていた気象の専門家。 共著者の大木氏は科学書・教科書の編纂を得意とする編集者です。 「気象学」は高校理科では選択の少ない「地学」に含まれているので、気象については中学以来ご無沙汰の方がホトンドではないでしょうか […]
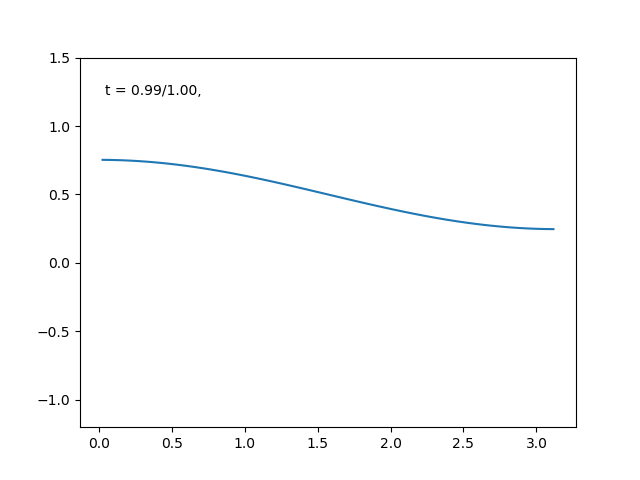
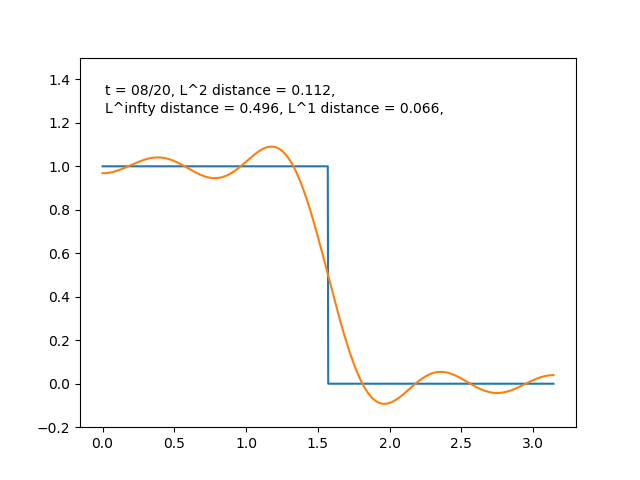
前回記事フーリエ変換とは無限次元空間の直交分解のひとつであるでは、 三角関数の族は関数空間の正規直交基底になっているよ！ フーリエ変換はそれらへの直交分解だよ！ ということを説明しました。 今回はさらに、 フーリエ変換は自然現象を捉えるのに役に立つよ！！ ということを説明していきたいと思います。 フーリエ変換で熱の拡散を捉えてみよう 明日の東京の気温はどれくらいだろうか？ エアコンはどこに置くと冷 […]
DNA、遺伝子、ゲノム、エピジェネティック…… 混乱しがちなこの辺りの用語を、備忘録的にサクサクとまとめてみました。 「DNA」と「遺伝子」の違いは？ 簡単に言えば、 「DNA」は「物質としての名前」＝ハードウェア 「遺伝子」は「機能としての名前」＝ソフトウェア ということになります。 DNAとは「デオキシリボ核酸deoxyribonucleic acid」という物質の名前。 遺伝子 […]
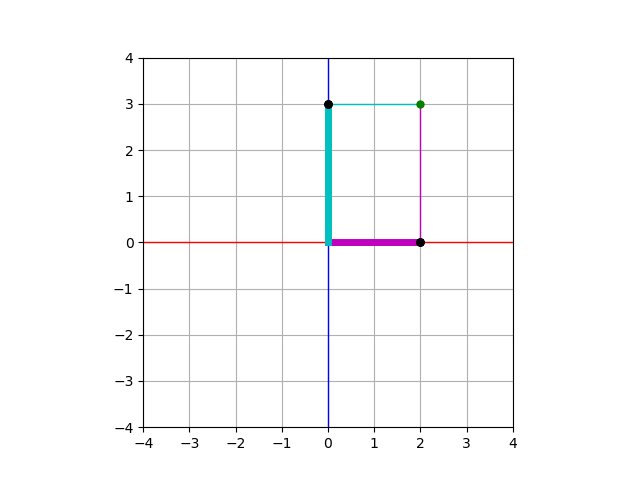
前回の記事では, 2次元のベクトルに対して, 内積を通して直交分解を理解しました. 2次元空間での内積 \((\cdot,\,\cdot)\) には, 大まかに言って次の3つの性質があります. (1) 任意の \(x\in \mathbb{R}^2\) に対して, \((x,\, x)\ge 0\)であり, さらに \((x,\, x)= 0\) と \(x=0\) は同値 (2) 任意の \(x […]
記事を3回に分けて, フーリエ級数展開は直交分解の一種だということをお伝えします. 直交分解って？ まずは私たちが認識しやすい次元空間を例に取り, 平面ベクトルを分解することを考えていきましょう. この記事では, 2平面ベクトル \(a\), \(b\) は列ベクトルとして書きます. つまり $$a=\begin{pmatrix}a_1\\a_2\end{pmatrix},\quad b=\beg […]
この記事は、前回に引き続き、下記のニュースを取り上げます。 田中耕一さんの技術、アルツハイマー早期診断への道開く：朝日新聞デジタル アルツハイマー病の高精度アミロイドβ血漿バイオマーカー | Nature | Nature Research さて、前回記事【「認知症」と「アルツハイマー病」って違うの？】では、アルツハイマー病と認知症の対比を通してまとめました。 特に以下の三点をおさら […]
【書評】 個体発生は進化をくりかえすのか 個体発生は進化をくりかえすのか 倉谷滋, 岩波科学ライブラリー, 2005/7/9 BACKGROUND ――対象 「個体発生は系統発生をくりかえす」 ――有名なヘッケルの言葉であり、「反復説」と呼ばれてる仮説を端的に語るものです。 「個体発生」とは、受精卵が細胞分裂と分化を繰り返して、一つの個 […]
先日、こんな科学ニュースが流れてきました。 田中耕一さんの技術、アルツハイマー早期診断への道開く：朝日新聞デジタル 私も興味があって精読したかったので解説記事にしようと思ったのですが、 「そもそもアルツハイマー病が何であるか知っている人って少ないのでは？」 という問題が噴出しまして。 「認知症とアルツハイマー病の区別もつかない状態で最先端の研究を説明なんて無理！」 とい […]
