前回の記事では, 2次元のベクトルに対して, 内積を通して直交分解を理解しました.
2次元空間での内積 \((\cdot,\,\cdot)\) には, 大まかに言って次の3つの性質があります.
(1) 任意の \(x\in \mathbb{R}^2\) に対して, \((x,\, x)\ge 0\)であり, さらに \((x,\, x)= 0\) と \(x=0\) は同値
(2) 任意の \(x,y \in \mathbb{R}^2\) に対して, \((x,\, y)= (y,\, x)\).
(3) 任意の \(x,y,z \in \mathbb{R}^2\), 任意の実数 \(\alpha,\beta\) に対して,
\((\alpha x +\beta y,\,z) = \alpha(x,\, z)+ \beta(y,\,z) \).
それぞれ (1)を正定値性, (2)を対称性, (3)を双線形性と呼びます.
3次元における内積は定義こそ異なりますが上の3つの性質を満たします. それぞれの内積の定義そのものよりもむしろ, これらの共通する性質が内積を内積たらしめていることは前回記事の計算からも伺えるのではないでしょうか.
今回は関数を分解する手法のうち代表的な1つであるフーリエ変換を, 内積のある関数空間の直交分解として導入します.
関数にも内積を導入しよう!
定義域が \((0, \pi)\) に制限された, 実数の値をとる関数 \(f\), \(g\) に対して, それらの内積 \((f,\,g ) \)を次のように定めましょう.
$$
(f,\,g) = \int_0^\pi f(x)g(x)\,dx
$$
さらに, 関数 \(f\) の大きさ \(\| f\|_2\) を
$$
\|f\|_2 = \sqrt{(f,\,f)} = \left(\int_0^\pi |f(x)|^2\,dx\right)^{1/2}
$$
によって定めます. \(\|\cdot\|_2\) をノルムと言います.
このように定義された内積ははじめに書いた内積の満たすべき性質を形式的には満たしていそうです.
とはいえ, 関数の選び方は何でもよいというわけにはいきません. 例えば,
$$
f(x)= 1/x
$$
という関数を考えると, そのノルムは広義積分
$$
\lim_{\varepsilon\rightarrow 0}\int_\varepsilon^\pi |f(x)|^2\,dx
$$
が発散してしまうため具合がよろしくありません. また,
$$
f(x)=
\begin{cases}
1,\quad \textrm{$x=\frac{\pi}{2}$のとき}, \\
0, \quad \textrm{それ以外のとき}
\end{cases}
$$
という関数を選ぶと, 一点はどんな小さな幅よりも小さいので積分には影響を与えず,
$$
\|f\|_2 = 0
$$
となることから内積の性質のうち正定値性を満たさない例となっています.
なので内積として対象とする関数を適度に制限する必要があります.
一方で制限の仕方によってはまた別の問題が起こりえます. 例えば連続かつ有界な関数に制限することにしましょう. すると, \((\cdot,\,\cdot)\) は内積になりますが, 関数列 \(f_n\) を
$$
f_n(x) =
\begin{cases}
0,\quad \textrm{$0 < x \le 1$のとき}, \\
n(x-1), \quad \textrm{$1 \le x \le 1+ \frac{1}{n}$のとき}, \\
1, \quad \textrm{$1+ \frac{1}{n} \le x < \pi$のとき}
\end{cases}
$$
と定めると, その(内積から定まるノルムによる)極限は
$$
f(x) =
\begin{cases}
0,\quad \textrm{$0 < x \le 1$のとき}, \\
1, \quad \textrm{$1 < x < \pi$のとき}
\end{cases}
$$
となるはずです.
しかしながらこれは明らかに不連続点を含む関数になっており, 連続かつ有界という要請を満たさなくなっています. つまり, 極限操作について”もろい”関数空間となっており, 一般論を構築するのには不向きなものになっています(逆に言うと、そういうことを考えるつもりがないならあまり気にしなくてもいいと思う)
このあたりを解消する方法(だけではないが)に, ルベーグ積分があります. これは大学の学部3年生くらいでたっぷり時間を掛けて勉強をする代物なので, 詳しく知りたい方は専門の教科書を読みましょう. 猪狩惺「実解析入門」
をオススメします.
結論としては(ルベーグの意味で)二乗可積分な関数のクラス \(L^2(0,\,\pi)\) を考えれば、さきほど挙げられたような疑問点はクリアされています. 以後は \(f\) として,
$$
\|f\|_2 = \left(\int_0^\pi |f(x)|^2\,dx\right)^{1/2}
$$
が有限な関数のみを扱っているんだなという風に理解してください.
関数の直交射影を考えよう!
やや天下り的ではありますが, 自然数または \(0\) である \(n\) に対して, \(L^2(0,\,\pi)\) に属する関数 \(e_n\) を
$$
e_n(x)=
\begin{cases}
\frac{1}{\sqrt{\pi}},\quad &\textrm{if $n=0$},\\
\sqrt{\frac{2}{\pi}}\cos{nx},\quad &\textrm{otherwise}
\end{cases}
$$
により定めましょう. 三角関数の計算から, \(e_n\) を集めた系 \(\{e_0,\,e_1,\,e_2,\,\cdots\}\) は
$$
(e_n,\,e_m)=
\begin{cases}
1,\quad &\textrm{if $n=m$},\\
0,\quad &\textrm{otherwise}
\end{cases}
$$
が示せるため(試してみよう!), これは正規直交系であることがわかります. 証明は難しい目なので省略しますが(調べてみよう!), さらに正規直交基底になっています.
つまり, \(d\) 次元空間の元 \(x\) が正規直交基底 \(\{\,e_1,\,e_2,\,\cdots,\, e_d\}\) により
$$
x = \sum_{k=1}^d (x,\, e_k)e_k
$$
と直交分解されるように, \(L^2(0,\,\pi)\) に属する関数 \(f\) は
$$
f = \sum_{k=0}^\infty (f,\, e_k)e_k
$$
と直交分解されます(ただしここでの等式は, 右辺の無限和は \(L^2\) の意味で左辺に収束するということ). このような直交分解をフーリエ級数展開(もしくはフーリエ変換)と呼びます.
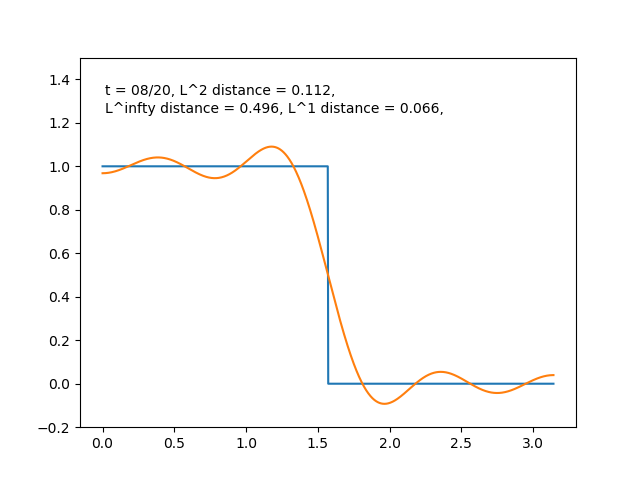
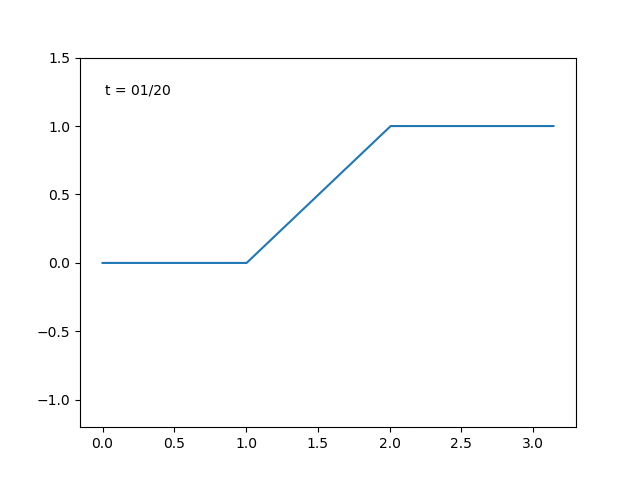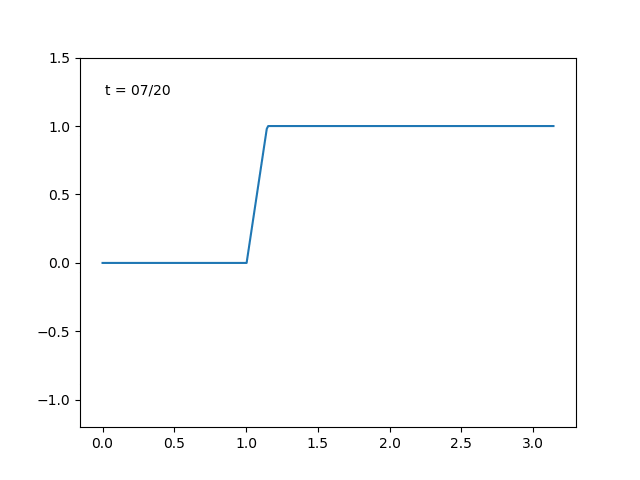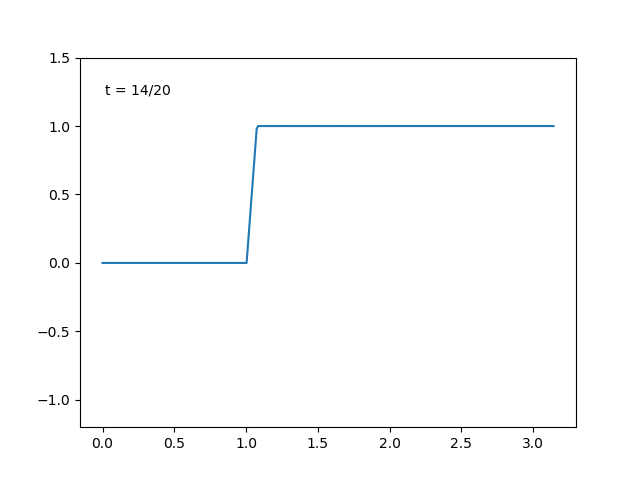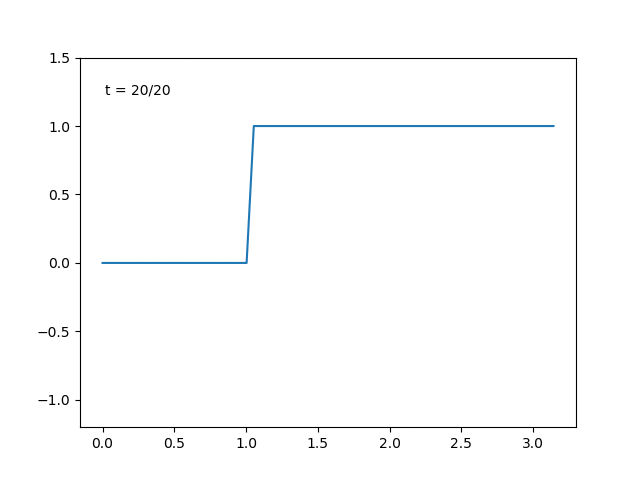
例えば, \(f\) がパルス型の関数のときは右辺の部分和
$$S_n(x)= \sum_{k=0}^t (f,\, e_k)e_k$$ において, \(t\) を増やすにつれて
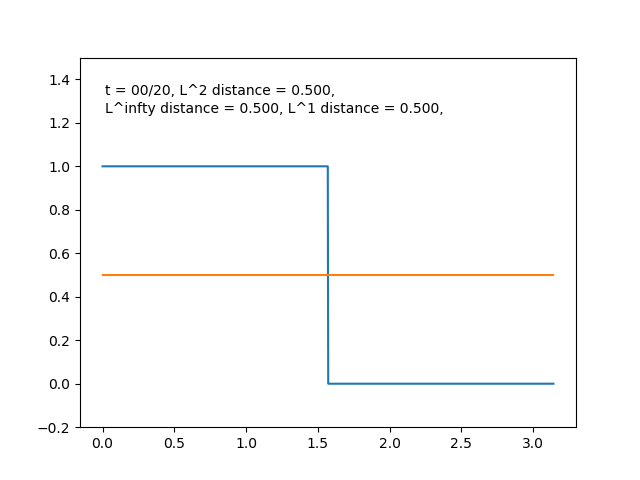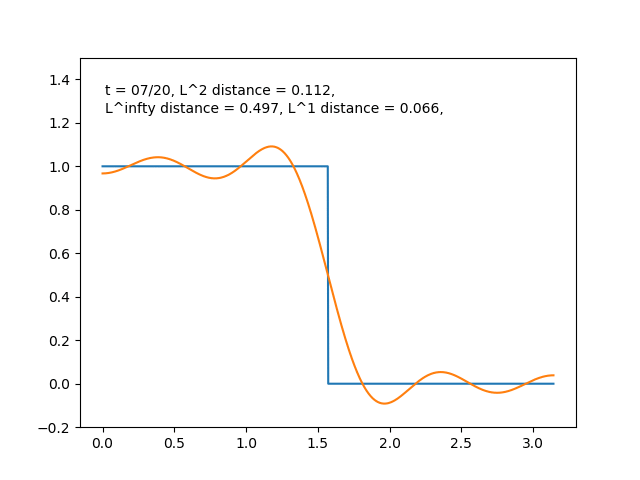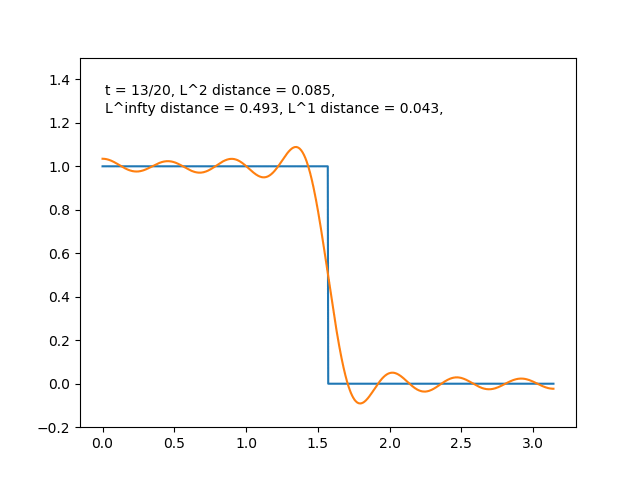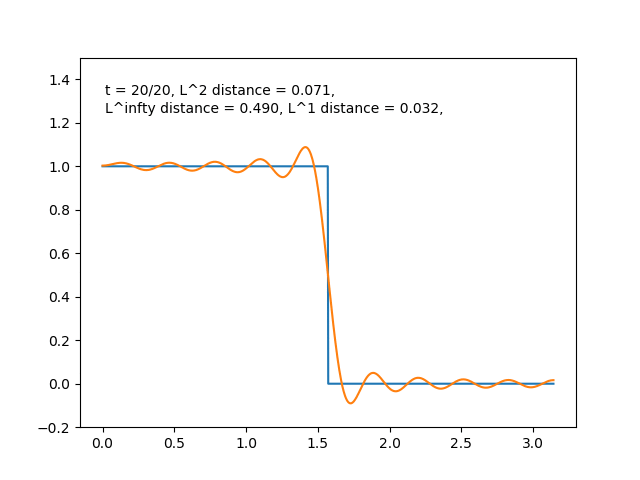
とどんどい良い近似になっている感じがします. \(f(x)=\sin{x}\) のときも同様に部分和をプロットすると,
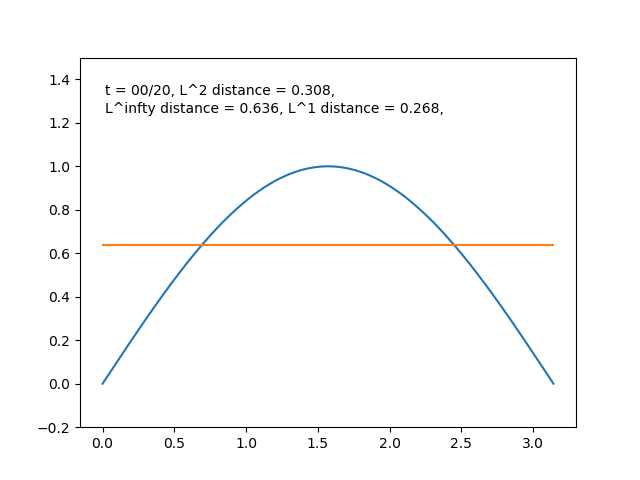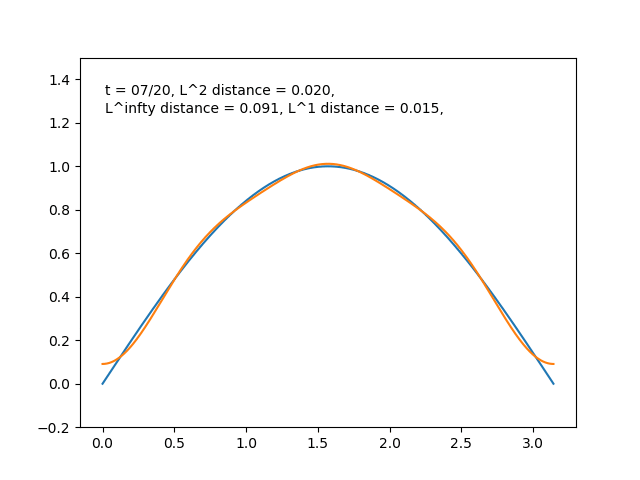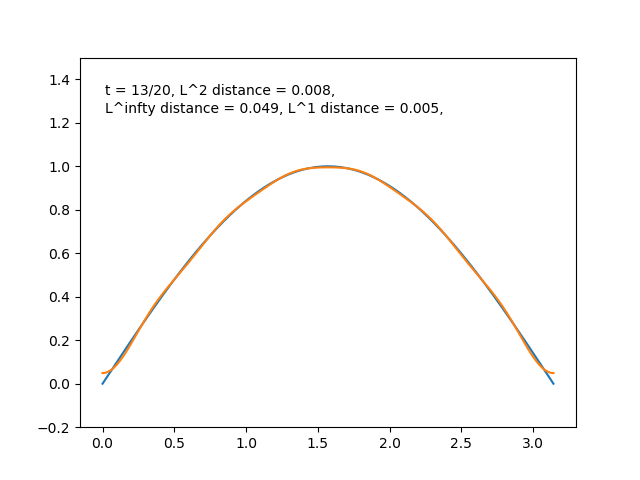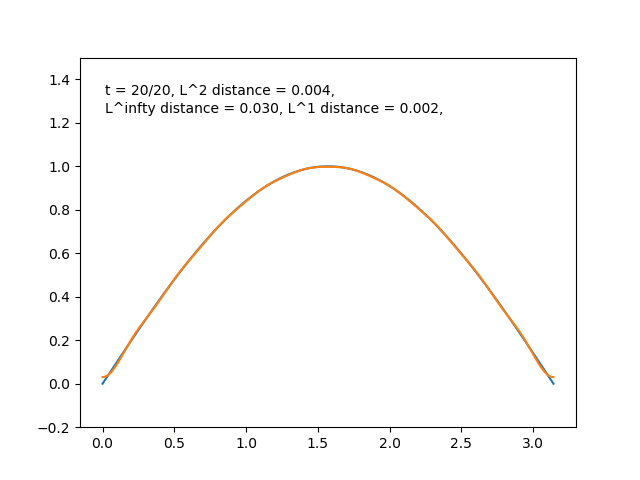
となり近似が進んでいる様子が分かります.
補足として, 有限次元では次元の個数だけ線形独立なベクトルを集めてくれば基底になっているのに対して, 無限次元ではそのアナロジーは成立しません. 例えば, \(e_0\) を抜かした無限個の関数を持つ正規直交系 \(\{e_1,\,e_2,\,\cdots\}\) は \(f(x)=1\) を近似できなくなっています.
このように完全性の証明は一筋縄ではいかない(つまり, 線形代数でよく知られた事実だけではうまくいかない)ことが多く, この場合は連続関数の稠密性とポワソン積分を用いた方法で証明することが出来ます. 詳しくは黒田成俊「関数解析」
の4章を調べることをオススメします.
兎に角これで, よく言われる, 関数空間が無限次元とはどういうことか?という問いも, ぼんやりとは理解できたのではないかと思います.
また, この段落についてはよい解説としてフーリエ級数展開をベクトルで直観的に理解する – Phys and Tipsがあるので, そちらもご参考にしてください.
他にも正規直交基底は存在するのでは?
有限次元で正規直交基底が1つに定まらなかったように, 無限次元でも同様のことが起こりえます. とりわけ, 三角関数らしくないものであっても正規直交基底になっており, それらを用いて直交分解ができます.
ラーデマハー関数列と自然数の2進展開を用いて表せるウォルシュ関数系もまた, \(L^2\) における正規直交基底になっています.
(分かりやすさのため, 定義域の区間は \( (0,1)\) に取り替えています.)
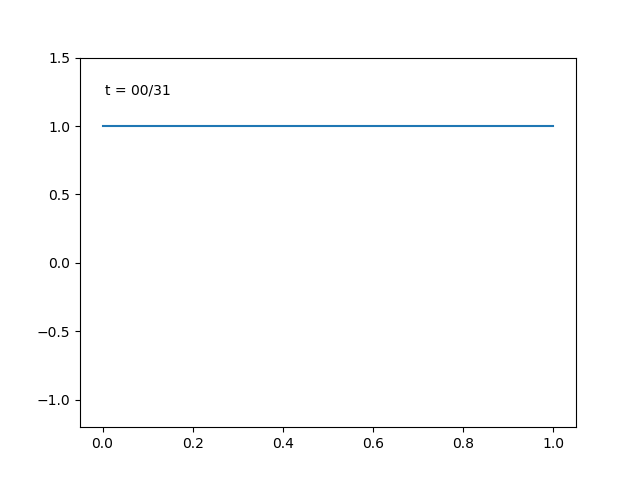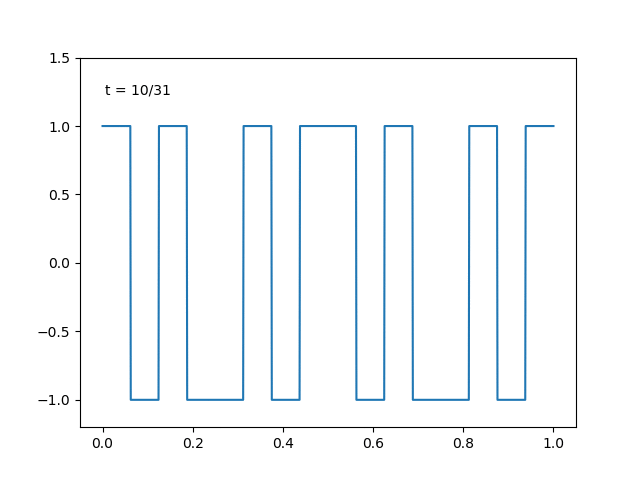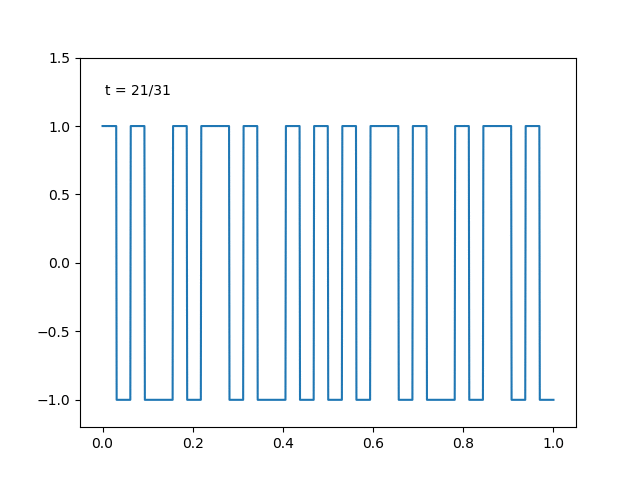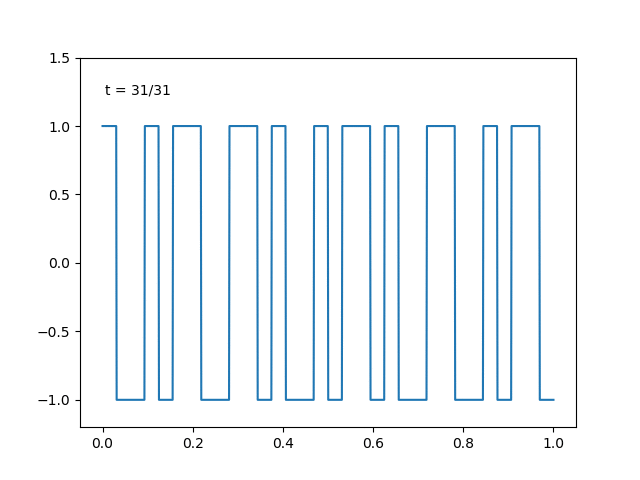
実際にこの関数系でも関数の直交分解は達成できます. 適当に二次関数を選んで,
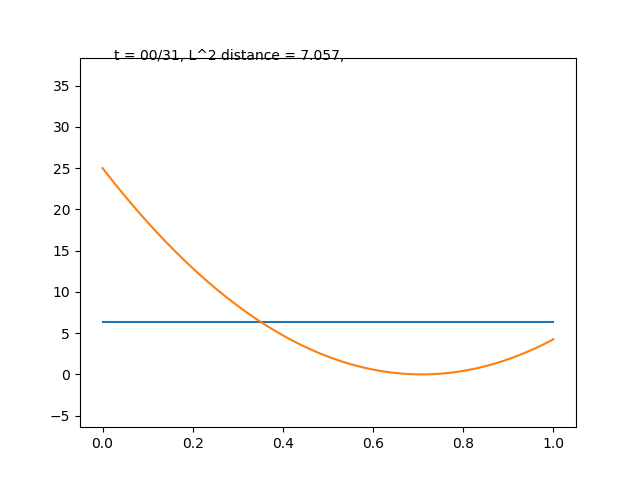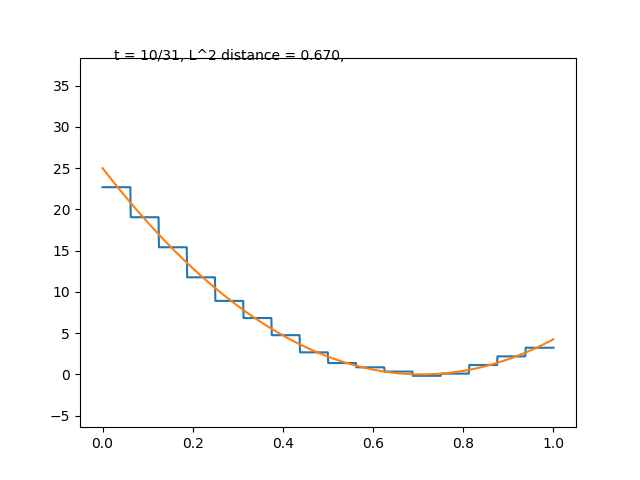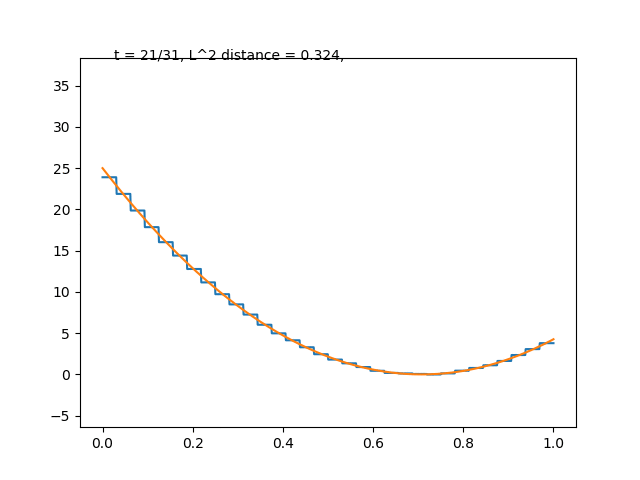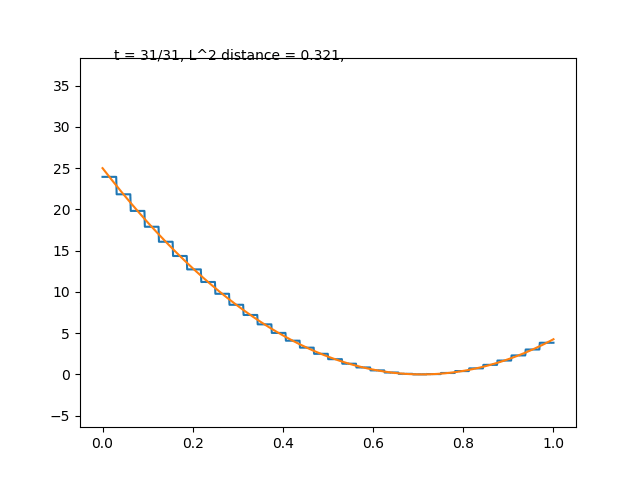
のように階段近似がなされます. このような変換はウォルシュ–アダマール変換と呼ばれ, 暗号や量子情報理論で活躍するようです.
他にも正規直交基底はあります. 例えばハール基底と呼ばれるものは, 三角関数では捉えきれない局所性を調べるのに使われ, ウェーブレット変換の基本をなすものとなっています.
では三角関数を用いたフーリエ級数展開がとりわけ有名になっているのではなぜでしょうか?次の記事では, フーリエ変換は偏微分方程式の文脈で非常に強力なツールになっていることを解説します.
わかばめ
最新記事 by わかばめ (全て見る)
- 常微分方程式の解の一意性が成り立たない例についてざっくりと。 - 2018年9月2日
- フーリエ変換は自然現象を捉えるのに便利である - 2018年7月21日
- フーリエ変換とは無限次元空間の直交分解のひとつである - 2018年5月30日