今回は
$$A=\begin{pmatrix} 5 &\sqrt{3} \\ \sqrt{3} & 3\end{pmatrix}$$
という行列を例に、線形代数で学ぶ固有値と固有ベクトルについて理解を深めて行きましょう。
固有値と固有ベクトルを視覚的に理解する話として、次の記事も参考になります。
行列はベクトルをベクトルに写す写像と言えます。また、正方形を平行四辺形に写す写像と捉えることもできます。
行列同士の掛け算や、行列とベクトルの掛け算、二次の正方行列の行列式の計算方法くらいまでの知識を仮定して、直観的な理解を得ていきましょう。
疑問点や、コメントなどございましたら気軽にコメントを下されば幸いです。
固有値と固有ベクトルの定義(用語解説)
正方行列 \(A\) に対して、
\begin{equation}Av =\lambda v\end{equation}
を満たすスカラー \(\lambda\) を固有値, ゼロでないベクトル \( v\) を(固有値 \(\lambda\) に対応する)固有ベクトルと呼びます。
固有値と固有ベクトルの求め方
定義式をそのまま展開して求めることもできなくはありませんが、次の3ステップで計算をすることが多いです。
1. 固有多項式を求める
固有値と固有ベクトルの定義式から、何か得られる情報はないでしょうか?\(E\) を単位行列とします、つまり
$$E=\begin{pmatrix} 1&0 \\ 0 & 1\end{pmatrix}$$
とします。このとき、定義式の右辺を移項して、ベクトル \(v\) でまとめることにより、
$$(A-\lambda E) v = 0$$
という \(v\) に対しての一次連立方程式と同値になります。(注意:右辺の \(0\) は \(0\) ベクトル、つまり各成分がゼロのベクトルです。)
これから \(v=0\) 以外の解を探すのですが、仮に \( (A-\lambda E)\) の逆行列が存在する場合は、左から \( (A-\lambda E)^{-1}\) を掛けることによって \( v=0\) が得られてしまうため、これはアウトです。
したがって、行列 \( (A-\lambda E)\) は正則ではない、つまり行列式について \( |A-\lambda E|=0\) という性質が必要だということがわかりました。
ここで現れる \( |A-\lambda E|\) を行列 \(A\) の固有多項式といい、方程式 \( |A-\lambda E|=0\) を固有方程式といいます。
2. 固有方程式を解いて固有値を求める
得られた固有方程式 \(|A-\lambda E|=0\) を変数 \( \lambda\) について解きます。
固有多項式の次数は行列の次数と等しくなるので(虚数解、重解を含めて)固有値 \(\lambda\) が2つ得られます。
3. それぞれの固有値に属する固有ベクトルを求める
固有値 \( \lambda\) が得られたので、今度はそれぞれに対応する固有ベクトルを求めましょう。
このとき固有ベクトルは一意に定まりません。実は固有ベクトルについては方向については定まるものの、長さについての任意性があります。
なので、ここで長さが \( 1\) になるように調整しておきます。(別にしなくても固有ベクトルは求まっているのですが、そのありがたみは次回以降解説しようかと)
実際に固有値と固有ベクトルを求めてみる
\(A=\begin{pmatrix} 5&\sqrt{3} \\ \sqrt{3} & 3\end{pmatrix}\) の固有値と固有ベクトルを求めましょう。
固有多項式は、
\( \begin{align}|A-\lambda E| &= \begin{vmatrix} 5-\lambda & \sqrt{3} \\ \sqrt{3} & 3-\lambda \end{vmatrix}
\\
&=(5-\lambda)(3-\lambda)-\sqrt{3}\cdot\sqrt{3}\\
&=\lambda^2 -8\lambda+12\\
&=(\lambda-2)(\lambda-6)\end{align}\)
と変形できるので、固有値は \( \lambda=6,2\) です。
固有値 \( \lambda=6\) に対する固有ベクトルを求めましょう。
\( v_1=\begin{pmatrix}x\\y\end{pmatrix}\)とおくと、
\( \begin{align}(A-6E)v_1&=0\\
\begin{pmatrix}-1&\sqrt{3} \\ \sqrt{3} & -3\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}&=0\\
-x+\sqrt{3}y&=0\\
x&=\sqrt{3}
\end{align}\)
よって固有ベクトル \( v_1\) は実数 \( k\) を用いて、
\( v_1=k\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}\)
と表せます。
\( |v_1|= k\sqrt{3+1}=2k\)
より、長さが\( 1\) になるように \( k=\frac12\) として
\( v_1=\begin{pmatrix}\frac{\sqrt{3}}{2} \\ \frac12\end{pmatrix}\)
にしておきます。
続いて固有値 \( \lambda=2\) に対する固有ベクトル \( v_2\) を求めましょう。こちらは同様の計算により、
\( v_2=\begin{pmatrix}\frac12 \\-\frac{\sqrt{3}}{2}\end{pmatrix}\)
となることがわかりました。したがって行列 \( A\) の固有値、固有ベクトルは
$$ (\lambda,v)= \left(6,\begin{pmatrix}\frac{\sqrt{3}}{2}\\ \frac12\end{pmatrix} \right), \,\left(2,\begin{pmatrix}\frac12 \\-\frac{\sqrt{3}}{2}\end{pmatrix} \right)$$
となります。
3. 固有値、固有ベクトルの”意味”を考える
固有値、固有ベクトルの定義から、次の等式が成り立ちます。
\begin{equation}Av_1 = 6 v_1\end{equation}
この等式は、\(v_1\) は行列 \(A\) を施すことによって方向を変えずに6倍拡大されることをあらわしています。
同様に、\(v_2\)は2倍されていることがわかります。つまり、行列は固有ベクトルの向きを変えないことがわかりました。
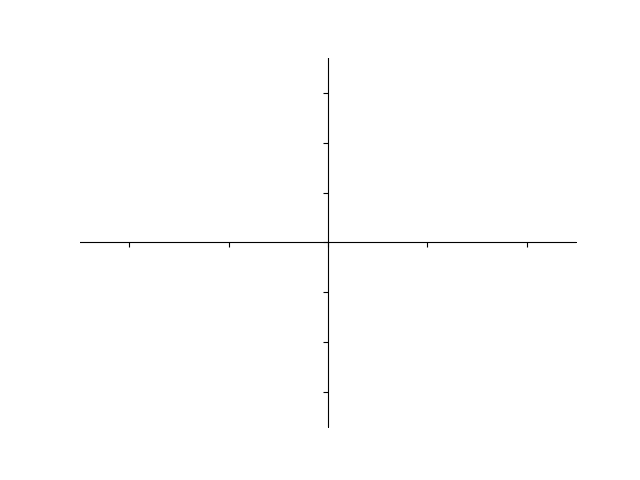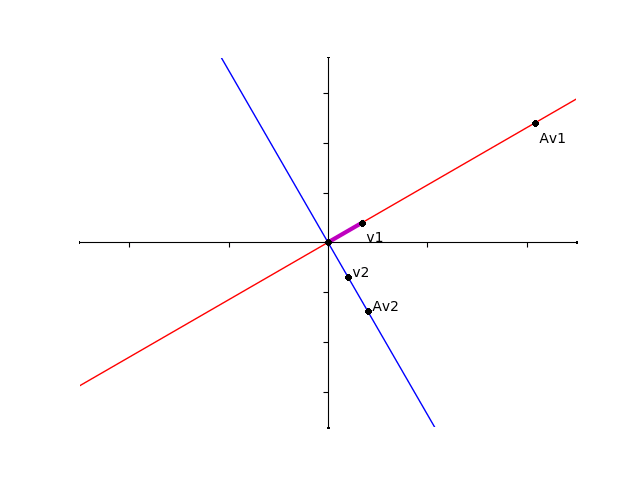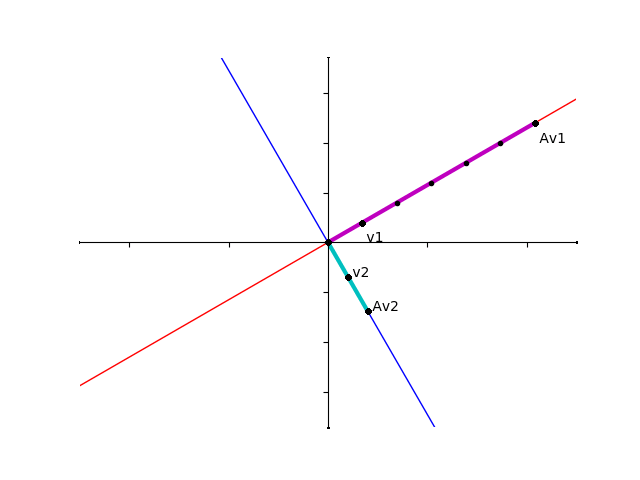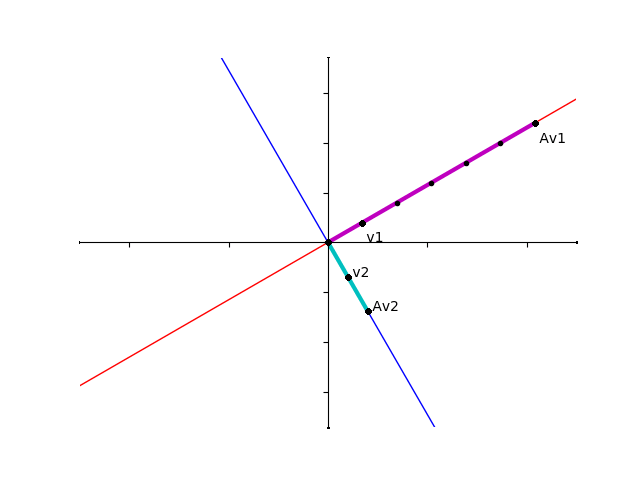
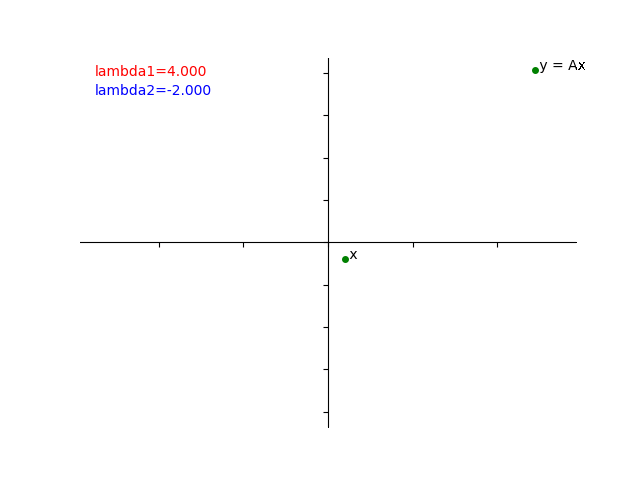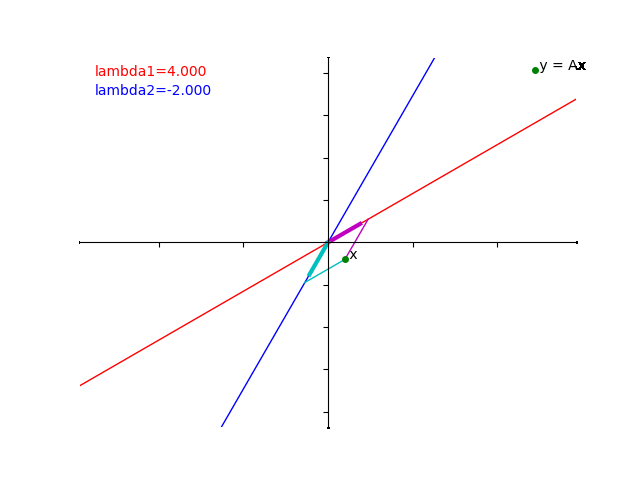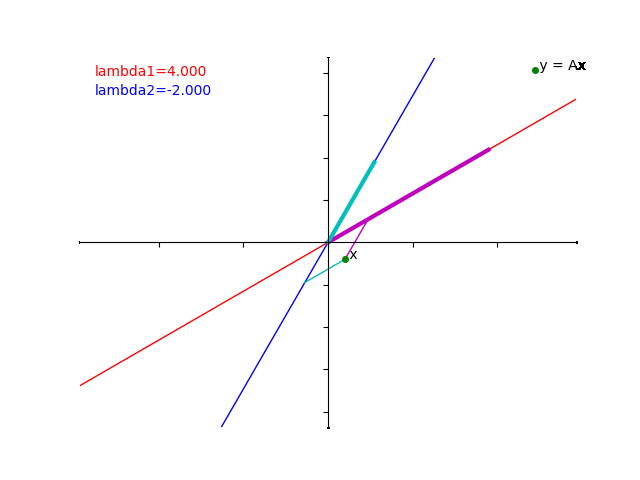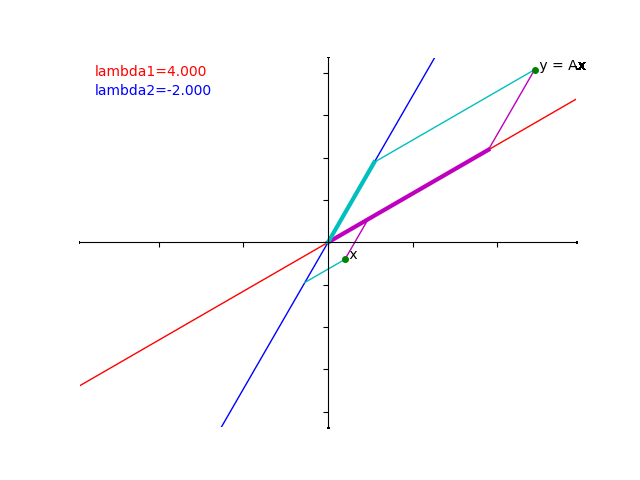
赤い線と青い線はそれぞれ \(\lambda_1,\lambda_2\) に対応する固有空間を表しています。
では、固有ベクトル以外の一般のベクトルは行列によってどのように移動するのでしょうか?
行列 \(A\) の固有ベクトルは一次独立のため、一般のベクトル \( x\) は 実数 \(s,t\) を用いて
$$ x = sv_1+tv_2$$
という形に書き直すことができます。このベクトルに行列 \(A\) を施すと、
$$\begin{align}Ax &=A(sv_1+tv_2)\\ &=sAv_1 + tAv_2\\ &=s\lambda_1 v_1 +t\lambda_2 v_2\\ &= 6s v_1 +2t v_2\end{align}$$
となります。
標語的に言うと、\(v_1\) と平行な成分は \(\lambda_1 = 6\) 倍引き伸ばされ、\(v_2\) と平行な成分は \(\lambda_2 = 2\) 倍引き伸ばされるということがわかりました。
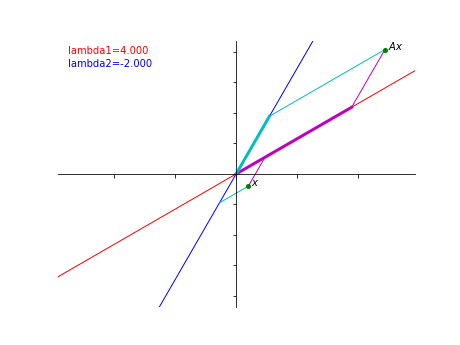
下のアニメーションは、\(x=\begin{pmatrix}0\\1\end{pmatrix}\) と \(y=Ax=\begin{pmatrix}\sqrt{3} \\3\end{pmatrix}\) の関係を gif で再現したものです。

\(x\) からそれぞれの固有空間に射影をしたあとに、赤い線にそって6倍、青い線にそって2倍したものが \(Ax\) ということがおわかりいただけたでしょうか?
4. おまけと次回予告
今回の例として扱った行列 \(A\) は対称行列であるため、固有ベクトルは直交していました。
しかし、このようなビジュアライズはもっと一般の行列に(固有値が単純かつ実数であれば!)も適応できます。
対称行列については、固有値についての別の特徴付けも得られます。次回はそういう話をしようかと思います。
わかばめ
最新記事 by わかばめ (全て見る)
- 常微分方程式の解の一意性が成り立たない例についてざっくりと。 - 2018年9月2日
- フーリエ変換は自然現象を捉えるのに便利である - 2018年7月21日
- フーリエ変換とは無限次元空間の直交分解のひとつである - 2018年5月30日