ちりつもFILE (β 「実際どうなの？」をちりつもするブログメディア。ただいまβ運用中。
解が無数にある常微分方程式 単純な常微分方程式についても, 解の一意性は必ずしも成り立たないことを本記事では紹介します: 次の常微分方程式の初期値問題を考えましょう \begin{align*} \begin{cases} \dfrac{dx}{dt}(t) = -2\sqrt{|x(t)|},\\ x(0) = 1. \end{cases} \end{align*} まずは, これを変数分離法を […]
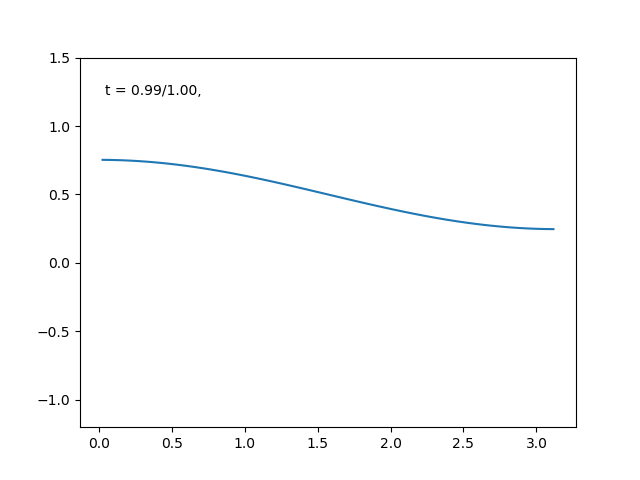
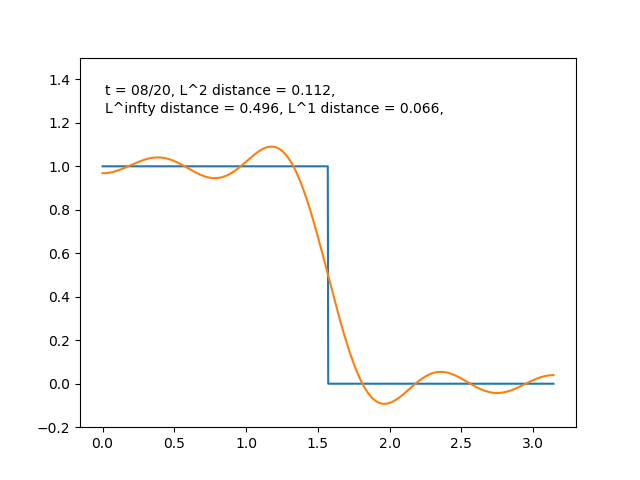
前回記事フーリエ変換とは無限次元空間の直交分解のひとつであるでは、 三角関数の族は関数空間の正規直交基底になっているよ！ フーリエ変換はそれらへの直交分解だよ！ ということを説明しました。 今回はさらに、 フーリエ変換は自然現象を捉えるのに役に立つよ！！ ということを説明していきたいと思います。 フーリエ変換で熱の拡散を捉えてみよう 明日の東京の気温はどれくらいだろうか？ エアコンはどこに置くと冷 […]
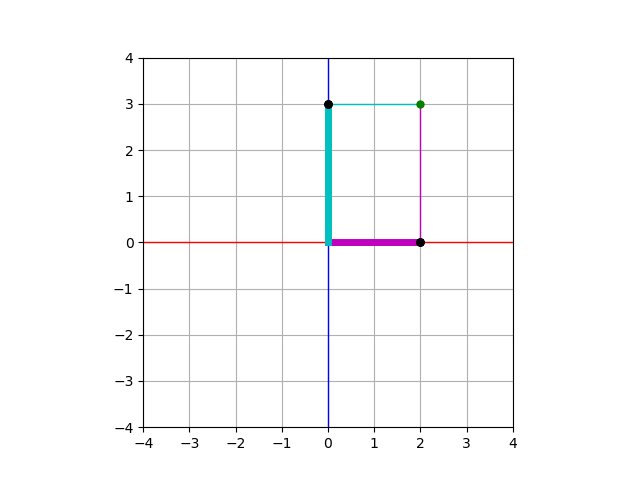
前回の記事では, 2次元のベクトルに対して, 内積を通して直交分解を理解しました. 2次元空間での内積 \((\cdot,\,\cdot)\) には, 大まかに言って次の3つの性質があります. (1) 任意の \(x\in \mathbb{R}^2\) に対して, \((x,\, x)\ge 0\)であり, さらに \((x,\, x)= 0\) と \(x=0\) は同値 (2) 任意の \(x […]
記事を3回に分けて, フーリエ級数展開は直交分解の一種だということをお伝えします. 直交分解って？ まずは私たちが認識しやすい次元空間を例に取り, 平面ベクトルを分解することを考えていきましょう. この記事では, 2平面ベクトル \(a\), \(b\) は列ベクトルとして書きます. つまり $$a=\begin{pmatrix}a_1\\a_2\end{pmatrix},\quad b=\beg […]
二次の正方行列に対して、具体的な計算を通して特異値分解についての解説を試みます。 早速ですが、復習問題です。 2つの行列 $$A=\begin{pmatrix}5 &1\\1&5\end{pmatrix},\quad B=\begin{pmatrix}4 &2\sqrt{3}\\0&2\end{pmatrix}$$ に対して、次の各問いに答えよ。 (1) それぞれの […]
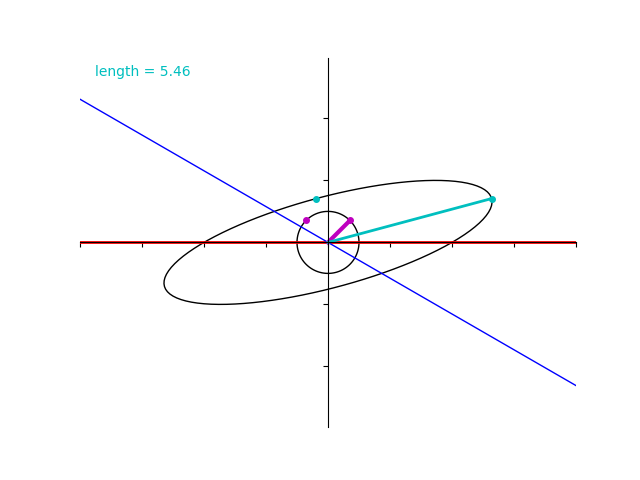
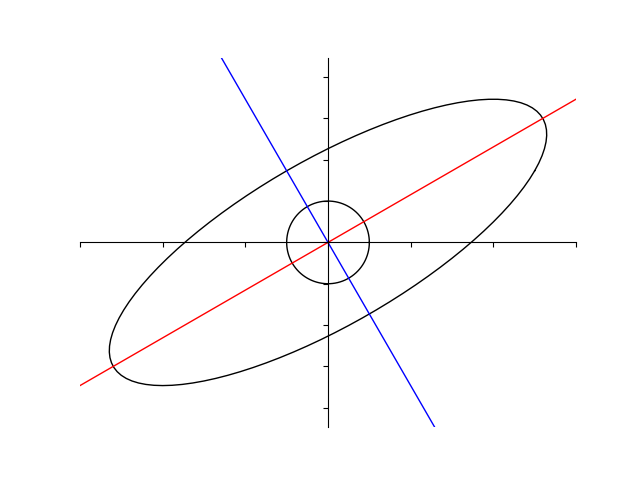
前回は行列は固有ベクトルの向きを変えないということを説明しました。 今回も引き続き、対称行列 $$A=\begin{pmatrix} 5 &\sqrt{3} \\ \sqrt{3} & 3\end{pmatrix}$$ を用いて、行列の固有値について解説をしていきます。 前回は行列は正方形を平行四辺形に写すものとして説明しましたが、今回は半径 \(1 \) の円（単位円）を写してみ […]
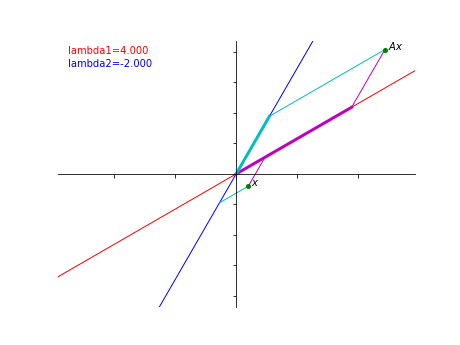
今回は $$A=\begin{pmatrix} 5 &\sqrt{3} \\ \sqrt{3} & 3\end{pmatrix}$$ という行列を例に、線形代数で学ぶ固有値と固有ベクトルについて理解を深めて行きましょう。 固有値と固有ベクトルを視覚的に理解する話として、次の記事も参考になります。 【数学】固有値・固有ベクトルとは何かを可視化してみる 行列はベクトルをベクトルに写す写 […]
