前回記事フーリエ変換とは無限次元空間の直交分解のひとつであるでは、
三角関数の族は関数空間の正規直交基底になっているよ!
フーリエ変換はそれらへの直交分解だよ!
ということを説明しました。
今回はさらに、
フーリエ変換は自然現象を捉えるのに役に立つよ!!
ということを説明していきたいと思います。
フーリエ変換で熱の拡散を捉えてみよう
明日の東京の気温はどれくらいだろうか?
エアコンはどこに置くと冷却効率がよいだろうか?
アツアツの鍋はどれくらい待てば持てるようになるだろうか?
今の状態から、将来の温度の様子がわかりたいですよね.
今回はその中でも単純な, 電熱線がどう冷めていくか?ということを考えていきます.
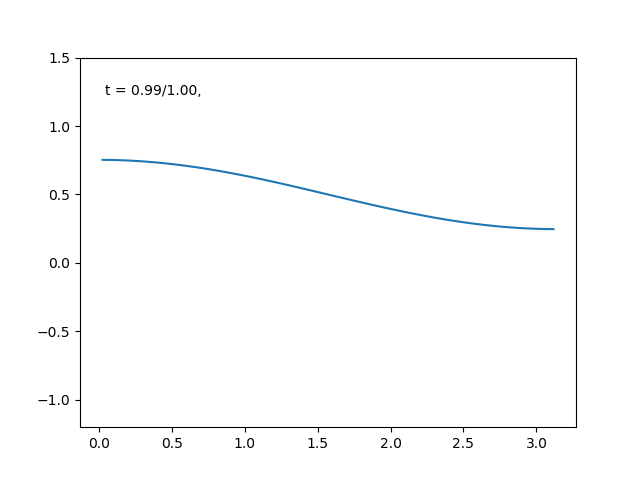
高さを温度としたときの熱拡散のアニメーションは, こんな感じです.
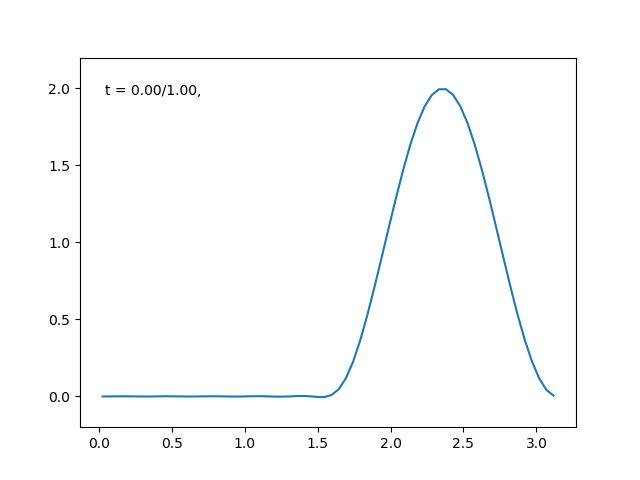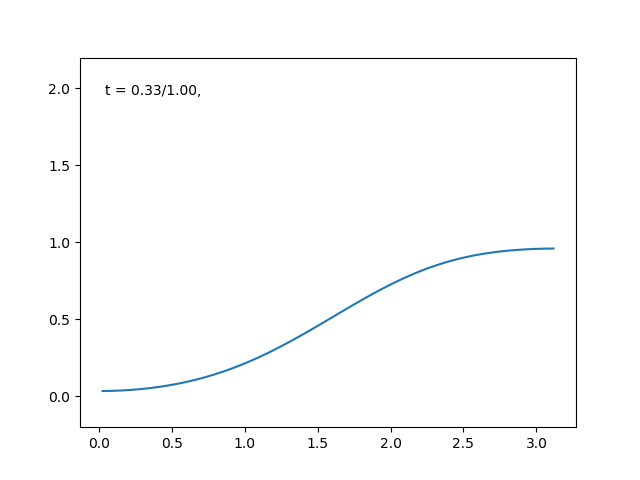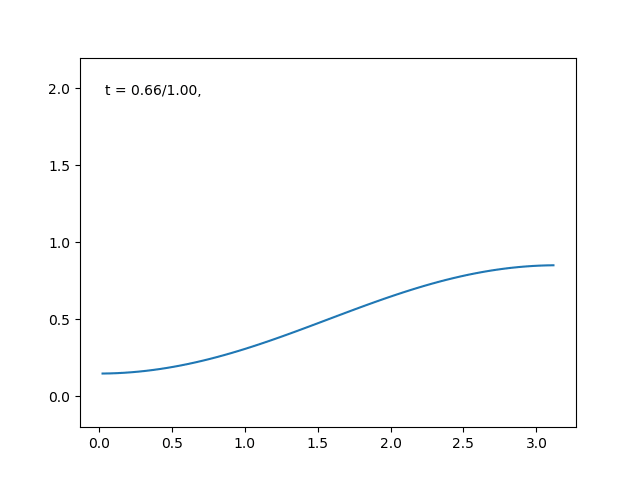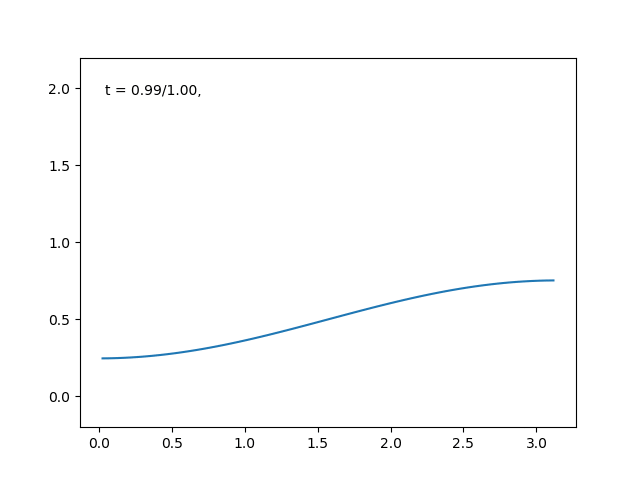
熱の拡散が満たすであろう法則を数式に直すと, 次のような微分方程式がモデルとして得られます.
\begin{equation}\left\{\begin{split}
\partial_t u(t,x) &= \partial_x^2 u(t,x),\quad & t>0, x\in (0,\pi),\\
\partial_x u(t,0) &= \partial_x u(t,\pi) = 0, \quad & t >0,\\
u(0,x) &= f(x), \quad & x \in (0,\pi).
\end{split}\right.\end{equation}
また, 方程式は上から順番に, 「熱は熱いところから冷たいところに伝わる」, 「端点では断熱」, 「ある時刻での温度はわかっている」ことを数式で表しています.
すなわち, 時刻 \(t=0\) ,位置 \(x \in (0, \pi) \) での温度分布 \( f(x) \) がわかっているします.
このとき, 時刻 \(t\), 位置 \(x\) における温度分布を表す未知関数 \(u= u(t,x) \) は上の方程式に従っているとして, それを求めていこう, という立場です.
\(e_n\) を前回記事で定義した \(L^2(0,\pi) \) の正規直交系として, \(f\) のフーリエ係数 \( c_n = (f, e_n)\) により,
\begin{equation}
f = \sum_{n=0}^\infty c_n e_n
\end{equation}
と与えられるとしましょう. さらに, 計算の見通しをしやすくするために, 新たに係数を \( a_n\) により与えて,
\begin{equation}
f(x ) = \sum_{n=0}^\infty a_n \cos{(nx)}
\end{equation}
とも表せていることとしましょう.
この微分方程式の解は次のように与えられます.
\begin{equation}
u(t, x ) = \sum_{n=0}^\infty e^{-n^2 t}a_n \cos{(nx)}
\end{equation}
では, 確かめてみましょう. 実際, \( e^{-n^2 t}a_n \cos{(nx)}\) を変数 \( t\) について1階微分をすれば,
\begin{equation}
-n^2 e^{-n^2 t}a_n \cos{(nx)}
\end{equation}
を得ます. 一方, 変数 \( x\) について1階微分をすれば,
\begin{equation}
-n e^{-n^2 t}a_n \sin{(nx)}
\end{equation}
であり, さらに変数 \( x\) について1階微分をすれば,
\begin{equation}
-n^2 e^{-n^2 t}a_n \cos{(nx)}
\end{equation}
となり, 各 \(n\) について第1式を満たしていることが分かります.
残りの2式も満たされることはすぐにわかりますね.
また, フーリエは \(u(t,x) = f(t)g(x)\) という変数分離が可能であると仮定して常微分方程式を導き出すことで解きました
境界条件が若干異なりますが, watanabechさんのブログが参考になります.
三角関数による表示は近似解を得るのにも便利!
初期値 \(f\) のフーリエ係数 \(a_n\) を求めることで, 近似解が求められます.
初期値のフーリエ係数を求めることで, 近似解が求められます. 適当な大きさの自然数 \(N\) に対して,
\begin{equation}
f_N(x) = \sum_{n=1}^N a_n\cos(nx)
\end{equation}
とします. 言い換えると, \(f\) を \(N\) の有限なモードで近似します.
初期値を \(f_N\) と取り替えて先ほどと同じ方法で解くと,
\begin{equation}
u_N(t, x ) = \sum_{n=0}^N e^{-n^2 t}a_n \cos{(nx)}
\end{equation}
が熱方程式を満たすことが分かります. これは有限個の \(n\) で和を打ち切っているため, 比較的コンピュータにも計算させやすい関数です.
さらに, 近似解 \(u_N\) と本来の解 \(u\) を比較しましょう. 時刻 \( t \ge 0\) における誤差 \(u(t,x) -u_N(t,x)\) を \(L^2\) のノルムで測ると,
\begin{align}
\| u(t) – u_N(t)\|_2^2
&= \left\| \sum_{n=0}^\infty e^{-n^2t} c_n e_n – \sum_{n=0}^N e^{-n^2t} c_n e_n \right\|_2^2\\
&= \left\| \sum_{n=N+1}^\infty e^{-n^2t} c_n e_n \right\|_2^2\\
&=\left( \sum_{n=N+1}^\infty e^{-n^2t} c_n e_n , \sum_{n=N+1}^\infty e^{-n^2t} c_n e_n \right)\\
&=\sum_{n=N+1}^\infty e^{-2n^2t} c_n^2
\end{align}
を得ます. 途中計算でノルムは自分自身との内積であることと, \(c_n\) が正規直交基底であることを用いています.
また, \( \sum_{n=0}^\infty c_n^2 = \|f\|_2^2 \) であり, \( n=N+1, N+2, \cdots\) のとき \( e^{-2n^2t} \le e^{-2N^2t}\) なので,
\begin{align}
\sum_{n=N+1}^\infty e^{-2n^2t} c_n^2
&\le e^{-2N^2t}\|f\|_2^2
\end{align}
つまり, \(\| u(t) – u_N(t)\|_2 \le e^{-N^2t}\|f\|_2 \) となり, 熱方程式の近似解は初期値を近似するモード数を表す \(N\) を増やすほど, 時間変数 \(t\) を大きくするほど精度がよくなることがわかります.
端点が一定温度の場合は, \( \sin \) で展開していく!
今度は電熱線の端点が何かに接触していて, 常に一定温度だという条件の下で解いていきましょう.
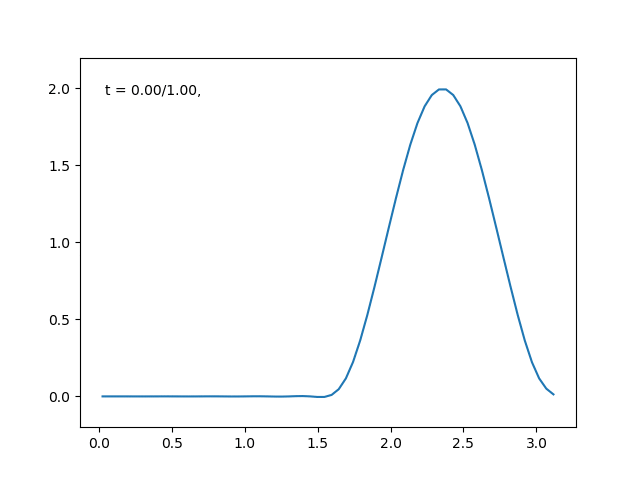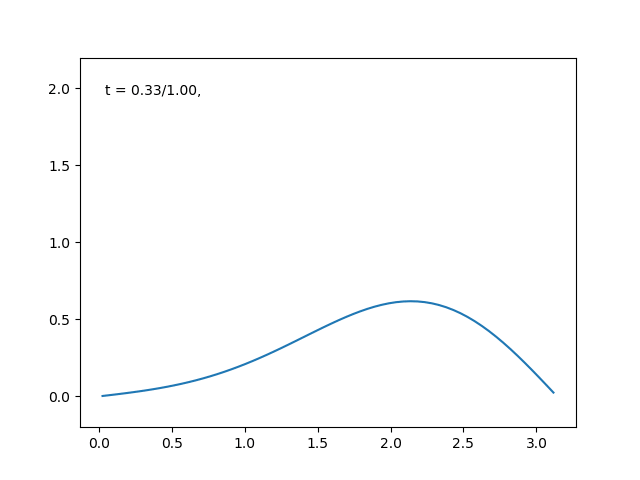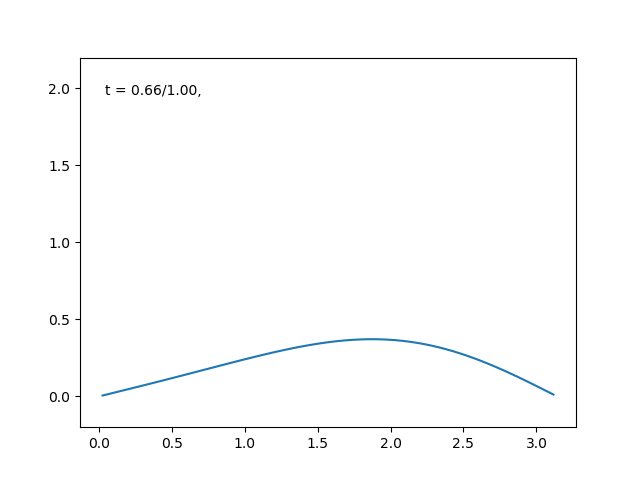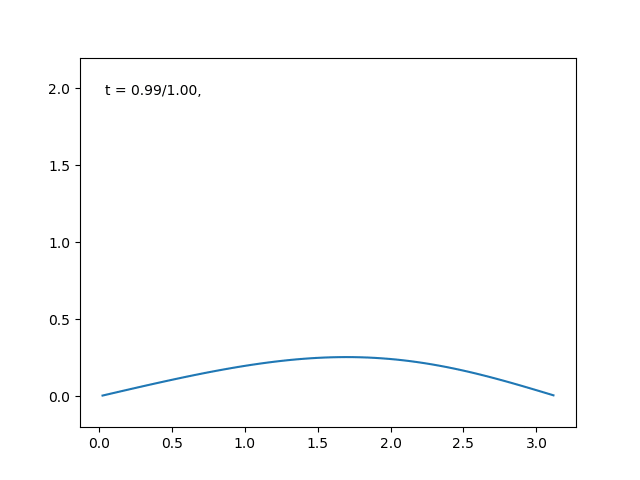
解くべき微分方程式は, 第2式を書き換えた, 次のものです.
\begin{equation}\left\{\begin{split}
\partial_t u(t,x) &= \partial_x^2 u(t,x),\quad & t>0, x\in (0,\pi),\\
u(t,0) &= u(t,\pi) = 0, \quad & t >0,\\
u(0,x) &= f(x), \quad & x \in (0,\pi).
\end{split}\right.\end{equation}
今回ように未知関数 \(u\) そのものの値を決めるような境界条件はディリクレ境界条件, 先ほどの断熱条件のように1階微分の値を決めるような境界条件はノイマン境界条件と呼ばれます.
第3式も \( t\in (0, \infty)\) の境界という意味では境界条件を与えていると言えますが, 時間発展する微分方程式においては初期条件と呼ぶことが多いです.
今回は初期値 \(f\) が正弦関数による直交展開
\begin{equation}
f(x ) = \sum_{n=1}^\infty a_n \sin{(nx)}
\end{equation}
と表せていることとしましょう.
この微分方程式の解は次のように与えられます(確かめてみてください).
\begin{equation}
u(t, x ) = \sum_{n=1}^\infty e^{-n^2 t}a_n \sin{(nx)}
\end{equation}
でも, もっと複雑な形にしてしまうと難しい(次回予告)
以上のように, 1次元の有限の長さをもつような領域では三角関数によるフーリエ級数展開が効果的だということがわかりました.
2次元や3次元の領域でも正規直交基底を見つければ簡単に熱の拡散を捉えられるはずだと思えてきます.
そのうえに, 誤差も指数関数的に減っていくので, 信頼できる数値シミュレーションも作れそうです.
ところが, 1次元では有界半区間, 半開区間, 実数全体の3種類の領域しかないのに比して, 高次元では無数の選択肢がありえます.
したがって, 一般の次元においては領域によっていろいろな正規直交基底が考えられるようになり, 今回のようにきれいに解くことが難しいであろうことが推測できます.
そこで, sin や cos のような, 2階微分をすると自分自身の定数倍になることと境界条件を満たすことの二点を満たすような正規直交基底を求めることを目標に, 次回の記事を書いていきます.
自分も数値シュミレーションのgifを作ってみたい!という方は,
Python で1次元の熱方程式を2通りの方法で解いてみた – わかばめにっき
Python を使ってお手軽に数学 gif を作ってみよう -@wakabame
が参考になるかもしれません.
わかばめ
最新記事 by わかばめ (全て見る)
- 常微分方程式の解の一意性が成り立たない例についてざっくりと。 - 2018年9月2日
- フーリエ変換は自然現象を捉えるのに便利である - 2018年7月21日
- フーリエ変換とは無限次元空間の直交分解のひとつである - 2018年5月30日