前回の記事では「知能」の研究の3つのアプローチを紹介しました。
1.Psychometric level (心理測定レベル)
2.Information-Processing level (情報処理レベル)
3.Brain level (脳レベル)
今回は「心理測定Psychometric」が生んだ最大の発明とも言える、「g因子」について紹介します。

全ての「知能」は正相関する
まず一般に、「知的能力を測るテスト」は、全て相互に正相関します。
これを事実として知っておいて下さい。
スピアマンはこの関係を学校のテストで見出しました。
英語(≒国語)、フランス語(≒外国語)、数学、音楽……
これらの学科試験の点数が、「いずれも(程度の差はあれど)正相関する」という結果を、実際の学生のテスト結果からスピアマンは示したのです。
これを分かりやすく言い換えてみましょうか。
個人ごとに多少の得意不得意はあっても、全体として「全教科で成績良い人」と「全教科で悪い人」が主流である
「〇〇は抜群に悪いけど〇〇は抜群に良い」という人は、皆無ではないが例外的である
単純に言えばそういうことです。
そしてこの現象は、WAISのような知能テストでも確認されました。
「語彙力を測るテスト」「複数の単語を短時間記憶しておくテスト」「暗算テスト」「空白に当てはまる図形を入れるテスト」「指定された記号を素早く探すテスト」「単純な質問にYes/Noで大量に答えるテスト」……
こうした一見無秩序なテスト群が、「どの2つをとっても正相関する」というのは一見して反直感的かもしれません。
しかしこの傾向は、その後も無数の心理実験で繰り返し再現されました。
暗算で100人中1位を取る人が、語彙力のテストでも1位を取れるかは分かりません。
しかし、「暗算で上位10%に入る人たち」の「語彙力の平均点」は、きっと一般の平均点よりは高いでしょう。
このような関係が、他のどんなテストについても同様に言えるわけです。
さて、このような事実を前にして、知能の研究者たちはこう考えました。
「人間にはそれぞれ『賢さの基礎パラメータ』とも言うべき『土台の知能』があって、言語や図形といった『分野ごとの能力』がそこに加わり、それが『各科目の能力』になるのではないか」
そして、この『賢さの基礎パラメータ』を「一般知能因子 general intelligence factor」と呼ぶことにしました。
他に、「g」「一般因子」「g因子」といった呼び方もありますが、いずれも同じものを指します。
知能研究の分野で「g」と言う場合、基本的にはこの「一般知能因子」のことを言っています。
『土台の知能』とも言うべき「一般因子 g factor」に対して、「国語が得意」とか「数学が苦手」といった得意・不得意を決めるのは、そこに上乗せされる『分野ごとの能力』です。これをスピアマンは「特殊因子 s factor」と呼ぶことにしました。
先の「様々な科目の能力」を「g」で解釈するというのは、簡単に言えば次のような図式です。
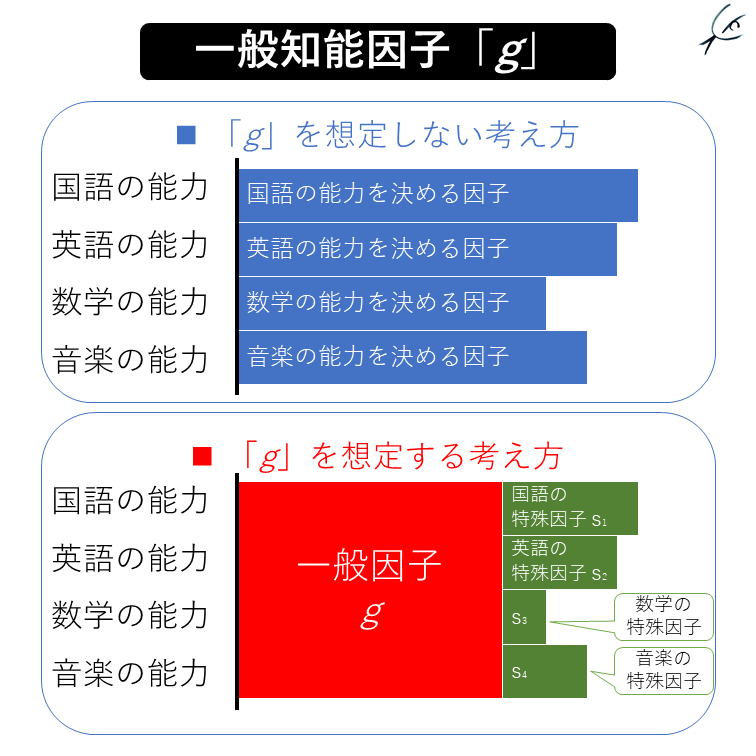
「g」をよく反映するテストは?
このように「g」は統計的に抽出される量的概念です。
「実証的なプロセスから出てきた数値」でありながら「実体として何であるかは依然として一致した見解が得られていない」という、何とも不思議なモノです。
ただ、統計学的な測定・解析から生まれるものである以上、それは常に知能検査の中で「定量的に位置付ける」ことができます。
WAIS-III(現状で普及している一般的な知能検査)では、いずれのテスト項目も相関係数(※)にして0.53~0.79程度の強さで「g」と相関することが明らかになっています。
相関係数0.79でgと最も高い相関を示したのは「算数の文章問題に暗算で答えるテスト」でした。
相関係数0.53でgと最も低い相関を示したのは「変換表に従って数字を速く正確に記号に置き換えるテスト」でした。
(WAIS-IIIの標準データより)
※ここでは正しくは「因子負荷量factor loading」と呼ぶべきですが、因子分析については別の記事で補足するので、ここではより一般的に理解されやすいと思われる「相関係数」という呼称を使うことにします。
某高知能団体の日本グループでは入会テストにRaven progressive matrices(RPM)を模したテストを使っているようです。
RPMは、一箇所が隠された図形配置の中で、隠された部分が何であるか当てるテストです。
ネットでよく見るタイプの知能テストだと思いますが、こういう感じのやつですね。

この手のテスト(RPM)は「g」と0.80程度で相関すると言われています。
この数字だけ見ると、「本格的な知能検査を行えない場合に一般知能因子gをRPMで代用する」というのは比較的マシなアイディアと言えそうです。
しかし、これによって算定される「上位2%」はあくまで「RPMの成績の上位2%」に過ぎません。
この基準で選出した集団は「知能指数でも平均の人口よりは優れた人たち」である可能性は高いものの、「一般知能における上位2%」とは決して言えません。
「正相関する」というのはその程度のことなのです。
更に、単一のテストでgを推定する場合に、高知能層ほど誤差が大きくなることも知られています。
これについては次の項で述べます
ちなみに、「語彙力のテスト」も、実は0.75ほどの高い値で「g」と相関する事がWAIS-IIIの標準化試験から判明しています。
これは先程のRPMとは真逆とも思える課題ですよね。
「図形の並びを推測するテスト」と「語彙力のテスト」の両方が共に「一つの知能因子」と高い相関を持つという事実は一見とても不思議に思えます。
しかし、これこそが「一般知能因子」という発見のすごさなのです。
「g」は踊る
ここまで読むと、「g」という概念がまるで強固な一枚岩のように思えるかもしれません。
しかし、統計概念の常として、「g」もまた測定の条件次第でいくらでもブレるということも知っておいて下さい。
一つの単純な例として、「同じテストを受けた数万人の受験者」の中から「5つの科目の合計点が400点ピッタリの人たちだけを抜き出した集団」を考えてみましょう。
この場合、「英語の得点」がずば抜けて高い人は、その分だけ「英語以外の得点の合計」が低いことになります。
つまり「英語の得点が高い人」の「数学の得点の期待値」は、集団平均より低いと予想されます。
お気付きでしょうか。
このような場合、「英語の点数と数学の点数」は「負の相関」となるわけです。
現実にはこんな特殊な集団抽出はほぼありませんが、例えば「大学入試」はどうでしょう。
「その大学の平均的な総合学力」と比べて「ずば抜けて高い総合点を出せる人」は上のランクの大学に行ってしまい、「ずば抜けて低い総合点しか出せない人」は不合格になります。
つまり、上記のような「全員の合計点がほぼ均一」な状況に近いわけです。
上記はあくまで思考実験ですが、「特定の大学の大学生」などでサンプルを集計すると、「g」が統計にはっきり現れないことがある、という指摘は実際にあります。
さて、話を一般人口に戻しましょう。
「gと各テストとの相関の強さ」は、実は「知能の高さ」によっても変わることが報告されています。
全体として、低得点層で見るとgの予測力は大きくなり、高得点層で見るとgの予測力は小さくなる傾向があるのです。
具体例で言い換えると、こういうことです。
「数学が”非常に悪い”子は、国語も”非常に悪い”可能性が高い」
「数学が”非常に良い”子は、国語も”良い方”ではあると予測されるが、”非常に良い”かは分からない」
……心当たりがあるでしょうか?
私も中学校の同級生などを思い出すと、「何の科目でも上位に入る人」は少なかったけど、「何の科目でも下位に入る人」というのは珍しくなかったなぁ……という実感があります。
この現象には色々な原因があると思いますが、
・下位層は『生物学的な要因』や『全般的な教育機会の欠乏』で差がつきやすい
→これらは全体的なパフォーマンスを下げる
・上位層は『追加的な教育投資』という部分で差がつきやすい
→これらは科目ごとに別個にパフォーマンスを上げる
という事例などを考えれば、ある意味で当然の結果とも考えられます。
更に単純な例で言えば、「学校に通えない子」や「ご飯を食べられない子」は「全部の科目の点数」が下がり、「塾で勉強した子」は「塾で勉強した科目の点数」が上がる、とも考えられます。
勿論、現実には様々な要素が絡み合っているのでこんなに単純ではありません。
しかし、「そのような傾向が生じる」という事実については、何となく実感を伴って納得して頂けたでしょうか。
理屈の部分は多分に仮定的な話が入っていますが、簡潔な事実として
・『特定の選抜がかかった集団』や『高知能の人たち』では『一般知能因子g』はそれほど顕在化しないことがある
という事実は覚えておく価値があるでしょう。
最後に。
ここまで述べた「g」は、あくまで統計的な存在です。
つまり「各能力値には正の相関がある」という単純な事実から想定された概念でした。
ここには、
・どうして知能はそんな仕組みになっているのか
・どんな脳活動と対応しているのか
といった視点は含まれていません。
仮説は諸説あるものの、実は未だに結論は出ていないのです。
「諸説」については後で機会がある時に説明することにしましょう。
本日はここまで。
おわりに
★ひとことまとめ
2. 知能の一般因子gが各能力に影響しているという発想は有用
★参考文献
・書籍
1.Earl Hunt: Human Intelligence(2010, Cambridge University Press)
村上 宣寛:
IQってホントは何なんだ?
日経BP, 2007
g因子について解説している一般向けの和書は非常に少ないです。
(おそらく正しく説明するためには統計の素養が必要になるからだと思われますが……)
こちらは既に紹介してきた本ですが、「g」について説明がされている数少ない和書です。
ただ、これも統計的な側面については用語を知っている前提でさらっと説明しているので、きちんと理解したい方は心理統計の本で別途学習する必要があります。
松岡 亮二:
教育格差
ちくま新書, 2019/7/5
こちらは統計解析とは少し違うアプローチ。
一般因子「g」は知能テストで見出される前に学科試験の成績の正相関から見出されたわけですが、「全ての科目に影響しうる因子」として「教育水準」の影響は見逃せません。
本書では、家庭環境が学力に与える様々な「格差」を扱っています。
家庭環境の影響がこれほど大きく、これほど多面的であるということを知ると、それだけで「あらゆる知的能力は正相関する」という話には納得できてしまうかもしれません。
★この研究会について
以下の書籍の輪読会をインターネット上にて定期開催しています。
Earl Hunt: Human Intelligence(2010, Cambridge University Press)
本記事は輪読会の内容を元に、メンバーのトークも盛り込んでサマライズしたものです。
トピックや話の流れは上記のテキストを踏襲していますが、内容は再解釈の上で大幅に加筆や再編を加えています。
なお、研究会に参加をご希望の方はこちらの記事をご覧ください。
この記事を書いた人
狐太郎
最新記事 by 狐太郎 (全て見る)
- AIサービスを活用した英文メール高速作成術 - 2023年3月28日
- 大学生・院生に便利なAIウェブサービスまとめ【2023年2月版】 - 2023年2月22日
- 「読書強者」が「速読」に価値を見出さない理由【隙間リサーチ】 - 2022年9月23日