記事を3回に分けて, フーリエ級数展開は直交分解の一種だということをお伝えします.
直交分解って?
まずは私たちが認識しやすい次元空間を例に取り, 平面ベクトルを分解することを考えていきましょう. この記事では, 2平面ベクトル \(a\), \(b\) は列ベクトルとして書きます. つまり
$$a=\begin{pmatrix}a_1\\a_2\end{pmatrix},\quad b=\begin{pmatrix}b_1\\b_2\end{pmatrix}$$
と書き表せることと約束します. また, \(a\) と \(b\) の内積を \(\left(a,b\right)\) と書き, 後に一般化することを意識してコサインを用いた定義
$$\left(a,b\right) = |a|\cdot |b|\cos{\theta}$$
のことは今回の計算では一旦忘れて,
$$\left(a,b\right) = a_1b_1 + a_2b_2$$
により定められていることとしましょう.
まずは直交分解の具体例として, ベクトル
$$a=\begin{pmatrix} 2\\3\end{pmatrix}$$
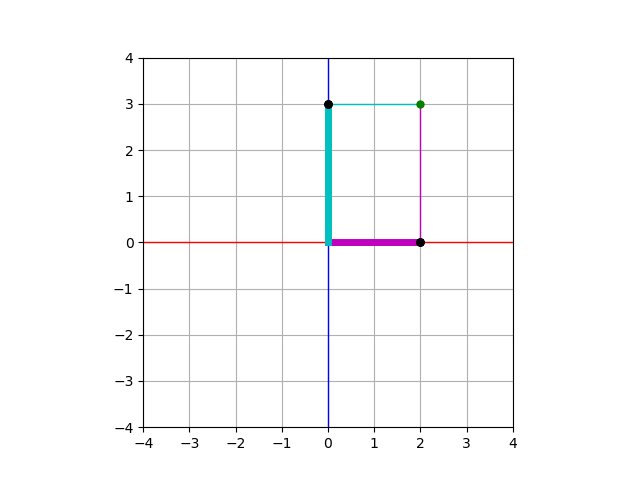
に対して初めて座標平面を習った時のことを思い出してみましょう. この点は, \(x\) 軸の正の方向に\(2\), \(y\) 軸の正の方向に\(3\)だけ進んだ点を表すのでした.
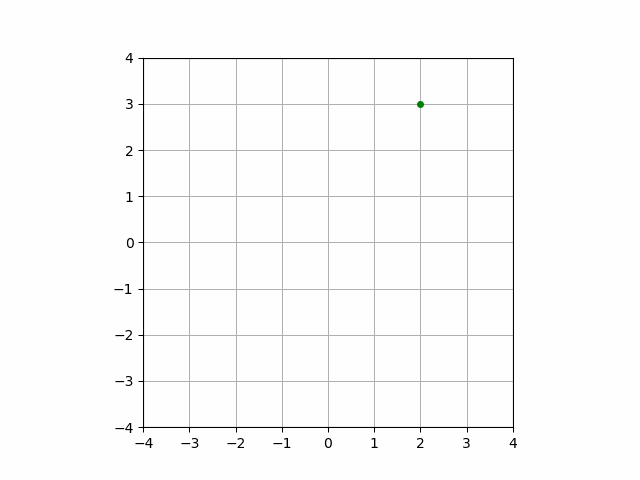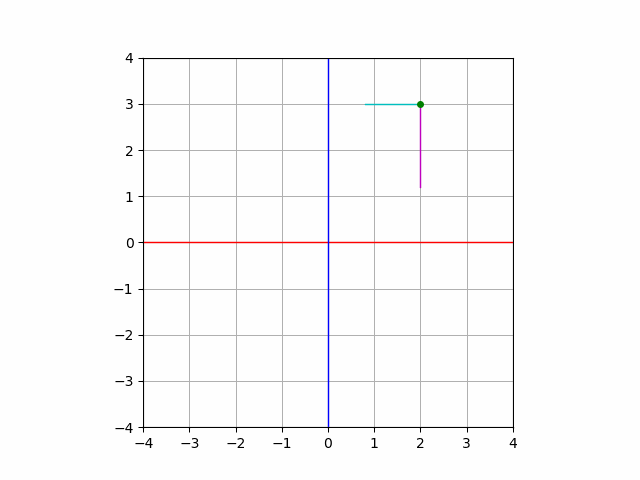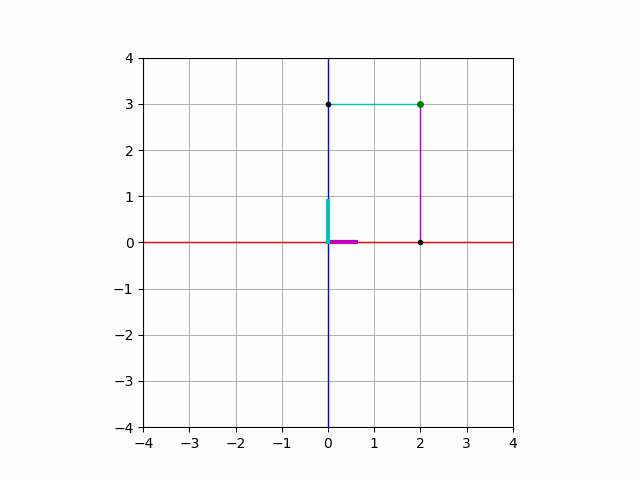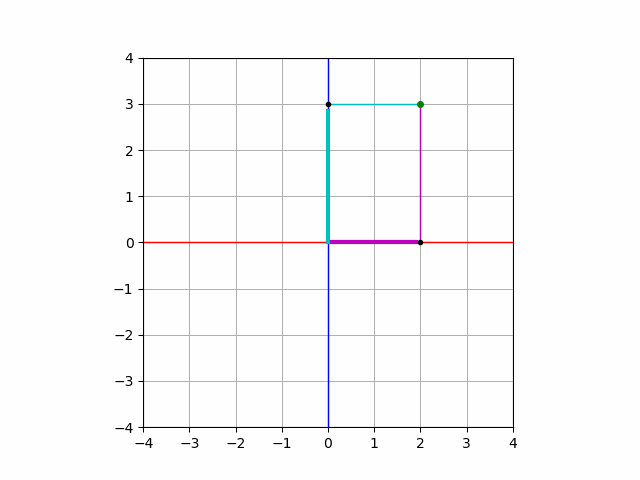
これを表現するような式変形をしてみましょう.
次のような計算は, 直交分解の1つです.
\begin{align}
\begin{pmatrix} 2\\3\end{pmatrix}
&= \begin{pmatrix} 2\\0\end{pmatrix}+\begin{pmatrix} 0\\3\end{pmatrix}\\
&= 2\times \begin{pmatrix} 1\\0\end{pmatrix}+3\times \begin{pmatrix} 0\\1\end{pmatrix}\\
&= \begin{pmatrix} 2\\3\end{pmatrix}\cdot\begin{pmatrix} 1\\0\end{pmatrix} \times\begin{pmatrix} 1\\0\end{pmatrix}
+\begin{pmatrix} 2\\3\end{pmatrix}\cdot\begin{pmatrix} 0\\1\end{pmatrix}\times \begin{pmatrix} 0\\1\end{pmatrix}
\end{align}
・・・かえって見にくくなってしまいましたね. 少し見通しを良くしましょうか. 最右辺の式は,
+ \textrm{y軸方向のおおきさ}\times \begin{pmatrix} 0\\1\end{pmatrix}$$
という形をしています. そこで,
$$e_1=\begin{pmatrix}1\\0\end{pmatrix},\quad e_2=\begin{pmatrix}0\\1\end{pmatrix}$$
とかくことにすると,
という等式が得られます. \(a\) が自分自身と \(e_1\), \(e_2\) によって表せていますね.
実はこれは全ての \(a\) について成り立つ恒等式であり, ベクトル \(a\) を右辺のように正規直交基底 \(e_1\), \(e_2\) の一次結合でかき表すことを直交分解といいます.
正規直交基底とは?
ここから, \(e_1\), \(e_2\) の性質を見ていきましょう. 先ほど定めた内積の定義を使うと, こんな性質がありますね.
\left( e_1,e_1\right) = \left( e_2,e_2 \right) =1 \\ \tag{2}
\left( e_1,e_2\right) = \left( e_2,e_1\right) = 0
\end{align}
これらの等式はそれぞれ, \(e_1\), \(e_2\) の長さが \(1\) の単位ベクトルであり, お互いに直交するベクトルになっていることを表します.
また, 等式 (1) を満たすベクトルのあつまりのことを正規系, 等式 (2) を満たすベクトルのあつまりのことを直交系といい, 両方を満たすものを正規直交系と呼びます.
さらに, 任意の \(a\) について, ある実数 \(\alpha_1\), \(\alpha_2\) が存在して
$$a = \alpha_1e_1 +\alpha_2 e_2$$
が成り立ち, かつ \(e_1\), \(e_2\) が一次独立であるとき, \(e_1\), \(e_2\) は基底であるといいます.
実は, 線形空間の次元とは基底の個数のことを表しています. 逆に言うと, 次元の個数だけ一次独立なベクトルを手に入れると, 必ずそれらは元の空間の基底になっています.
いまの場合は \(a_1 = (a\cdot e_1)\), \(a_2 = (a\cdot e_2)\) とおくことで等号を成立させることができ, その他方で直交性から一次独立であることがわかりますね.
このように正規かつ直交する基底のことを正規直交基底と呼ぶのです.
正規直交基底はただ1つじゃないよね
\(e_1\), \(e_2\) という軸と同じ方向を持つ単位ベクトルが正規直交基底となることがわかりましたが, 平面上の正規直交基底はこれだけではありません. たとえば,
$$e’_1=\begin{pmatrix}\frac{\sqrt{3}}{2}\\\frac12\end{pmatrix},\quad e’_2=\begin{pmatrix}-\frac12\\\frac{\sqrt{3}}{2}\end{pmatrix}$$
と定めていても, 正規直交基底であることの定義は満たし,
$$a = (a\cdot e’_1)e’_1 +(a\cdot e’_2) e’_2$$
という等式が常に成り立ちます.
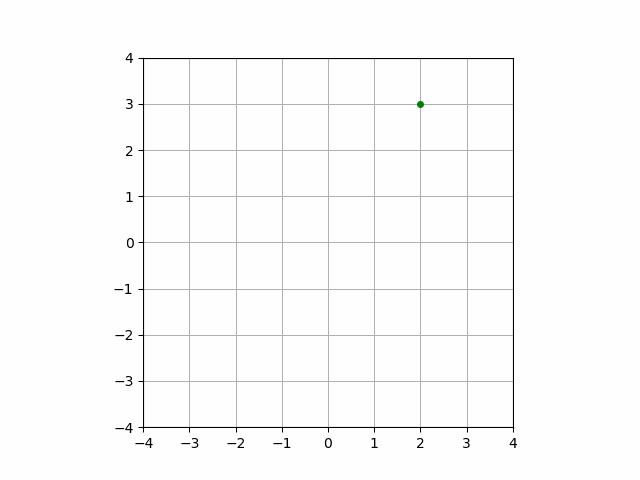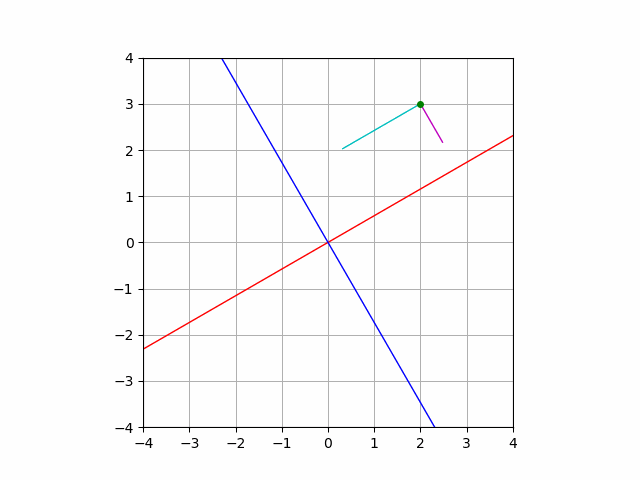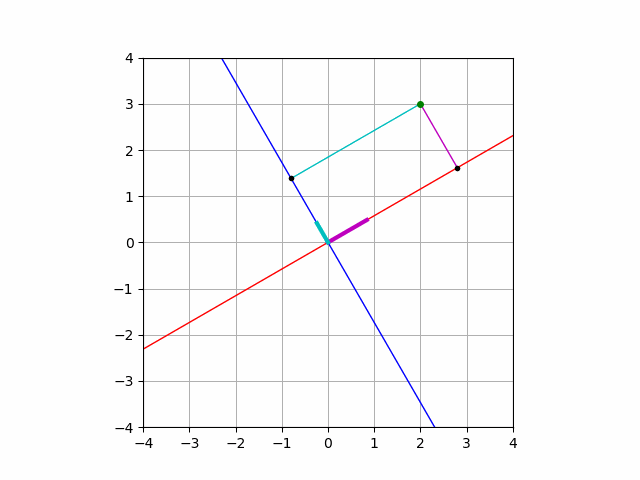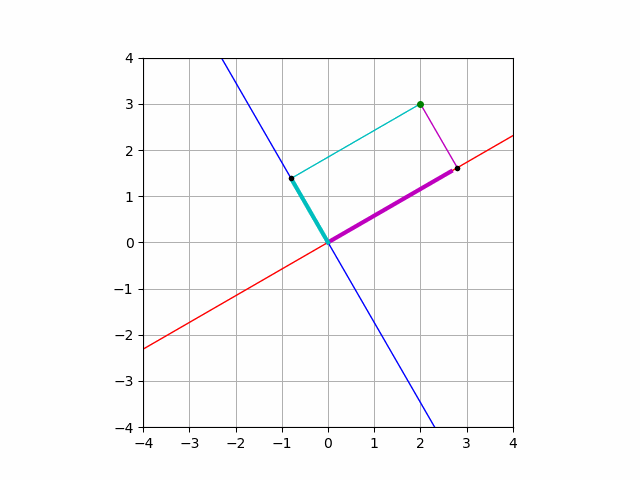
実際に計算して確かめることもできますし, このような紙芝居をみて理解することも可能です.
どんなときに直交分解ができるの?
ここでまとめましょう. ベクトルが直交分解できるためには, 正規直交基底が重要な概念であることがわかりました. 細かくみていくと,
(1) 土台となる空間に内積が定義されていること
(2) 正規直交系が見つかっていること
(3) 上の正規直交系が基底になっていること(つまり, 次元の数だけ見つかっていること)
が暫定的な答えとして良さそうです*1. また,
正規直交基底は必ずしも1通りではない
ということもわかりました. 今回の議論は2次元空間に留まらず, 高次元の線形空間に対しても同じように成り立ちます. 3次元の場合にはどのような正規直交基底が考えられるでしょうか?考えてみてください.
次回は無限次元空間の”住人”である関数に対しても似たような直交分解ができ, それがフーリエ級数展開なのだということを, 今回導入した有限次元空間における直交分解のアナロジーとして理解していきます.
1: 実は基底があればグラムシュミットの直交化法という方法で正規直交に書き直すことができるので, (2)は不要です
わかばめ
最新記事 by わかばめ (全て見る)
- 常微分方程式の解の一意性が成り立たない例についてざっくりと。 - 2018年9月2日
- フーリエ変換は自然現象を捉えるのに便利である - 2018年7月21日
- フーリエ変換とは無限次元空間の直交分解のひとつである - 2018年5月30日