高校数学で挫折者を生むヤマの一つ、「三角関数」。
世の中には「サイン・コサイン・タンジェントなんていつ使うのか」と言う人もいるくらい、「数学のなんだか難しいよく分からない記号」と思われがちです。
……が、実は三角関数って、日常生活にありふれている存在だったりします。
プログラマーや物理学者など「現象を数式にする」人たちにはもちろんのこと、機械や人体関節のような「回転角を扱う」場合にも重要です。
何より「音」を考えるならば三角関数は必須と言って良いでしょう。
「音」と無縁で生活している人は、我々の中にはほとんどいませんよね。
学校の数学では往々にして「数式的な定義」や「式変形」から入るので、「波」としての性質やビジュアルにまで気が付かずに挫折してしまうのかもしれません。
今回の記事は「グラフから入って数式にアプローチする」という「通常と逆の手順」で学び直すことで、「三角関数への苦手意識」を緩和できるのでは、という試みです。
「紙とペン」ではグラフを書くのがちょっと難しい三角関数ですが、コレを見ている皆さんなら、その問題は一発で解決します。
実はGoogle検索の検索窓にはグラフ描画機能が付いているからです。
折角なので今回はコレを活用します。
数式はコピペできるように付記しているので、興味のある数式はコピペして、細部の数字などを自分でいじってみてください。
なお、今回は三角関数の基本公式は適宜カンニングしつつ話を進めます。
うろ覚えの方は、以下のページも併読しつつお読み下さい。
・三角関数の定義
https://mathtrain.jp/sincostan
数学II「三角比」では三角形を使った1の定義で教わりますが、今回の話では単位円を用いて定義する2の定義を念頭に読んで頂く方が、直観的で分かりやすいかと思います。
(ただしツールの仕様上、今回は偏角はθでなくxで表します)
・三角関数の基本公式
https://mathtrain.jp/trig_basic
学校によっては大量の「公式」を覚えさせられるかもしれませんが、「sin, cos, tanの加法定理」の3つを覚えておけば十分です。他は全部そこから導出できるので。
この記事ではその3つの加法定理さえあれば分かるように書きます。
加法定理自体の導出は煩雑なので、証明省略して使わせてください。(証明こちら)
加法定理は、その導出が東大の入試問題にもなるくらいなので、先に暗記して使っている人の方が多いかと思います。私は何のひねりもなく「シンコスたすコスシン」「コスコスひくシンシン」「タンたすタンのいちひくタンタン」で覚えてました。

基本的な正弦波
とりあえず、まずはGoogleの検索窓にこれを放り込んでみます。
y = sin x
これだけでオッケー。
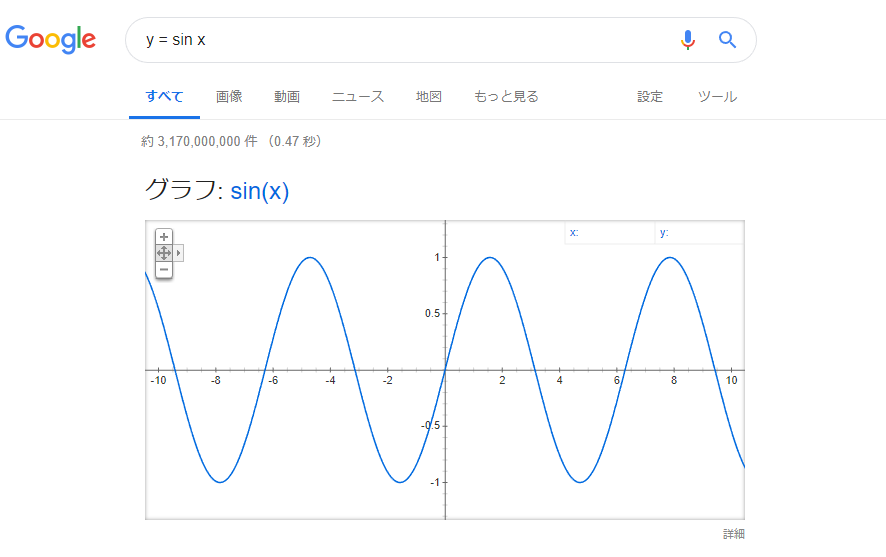
「,」で区切ると複数もいけます。最大4つまで。
y = sin x, y = sin 2x, y = sin 3x, y = sin 4x
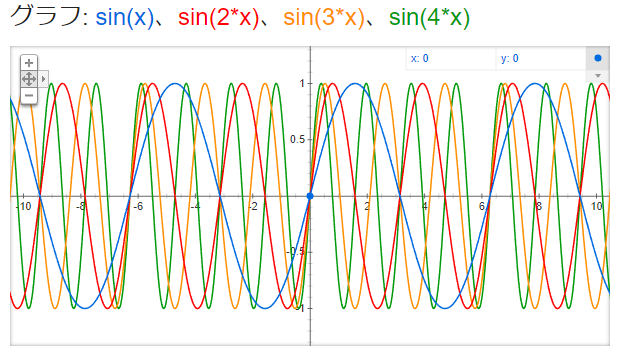
「y = sin(nx)」が「y = sin(x)をn倍の速さで振動させたもの」なのが分かりますね。
以後このような波の形は、平行移動や上下・左右方向の拡大・縮小をきかせたものも含め、まとめて「正弦波sine wave」と呼ぶことにします。
「y = sin(nx)」は周波数がy = sin xの整数倍なので、
「y = sin(nx)」のnに色々な値を代入したものを総和しても、
「x = 2πの周期性」を持つ関数になります。
y = sin x + sin 3x + sin 5x + sin 7x + sin 9x

y = sin x + 0.8 sin 3x + 0.6 sin 5x + 0.4 sin 7x + 0.2 sin 9x
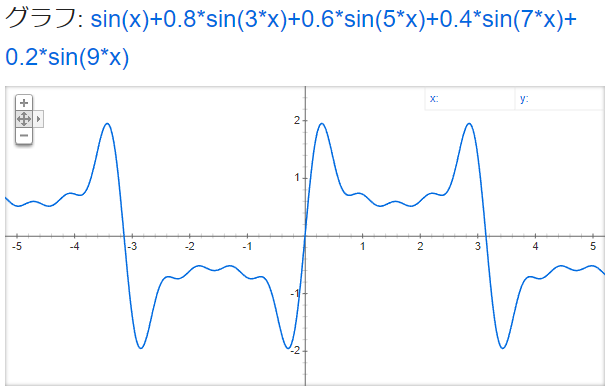
この周期性は、各項で「y = m * sin(nx)」だけしか使わなければ常に保たれます。
これは後で「音の波」を分析する時に重要になるポイントです。
今回の本筋ではありませんが、余裕があったら覚えておいて下さい。
これも正弦波?
今度はこんな数式を考えてみましょう。
y = sin x + cos x
慣れないとなかなか形が想像しにくいかと思います。
Googleに入れてグラフを出してみましょう
グラフが混み合って見づらければ左上のアイコンで適宜スケールをいじります。
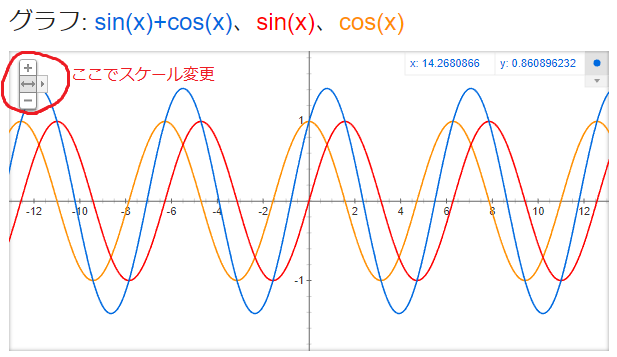
(参考のためにサインとコサインも残しました)
青色のy = sin x + cos x も何となくsinと同じ形っぽく見えますね?
これを証明してみましょう。
サインの加法定理の式を持ってきます。
(グラフ描画に使う式と混同しないよう、こっちは変数をa,b,cにします)
sin(a+b) = sin a cos b + cos a sin b
今はsin aとsin bの係数を同じにしたいので、「sin bとcos bが1:1になるような b」が欲しいです。「そういう都合の良いbがあると仮定する」と、こんな式が成立します。
sin(a+b) = sin a (sin b) + cos a (sin b) = (sin b)(sin a + cos a) ……①
ここで「sin bとcos bが1:1になるような b」について改めて考えます。
三角関数の定義に戻って考えてみると、「sin bとcos bが1:1になるような b」とは、「斜め45度(ラジアン表記でπ/4)」のことですね。

b = π/4、sin b = sin π/4 = √2/2を代入して、①の式はこうなります。
sin(a + π/4) = √2/2(sin a + cos a)
というわけで、さっきの黄色のグラフ
y = sin x + cos x
は、
y = sin x + cos x = √2 sin(a + π/4)
という「一つのサイン」で書けることが分かりました。
正弦波と同じ形に見えたのは偶然ではありませんでしたね。
ちなみに、任意のy = a sin x1 + b cos x2について、このような「一つのサインの式」で書き表すことが出来ます。興味のある方は下記のページでどうぞ。
https://mathtrain.jp/asinbcos
それではついでに、こんな式をグラフ化したらどうなるでしょう?
y = (sin x)^2
(※「^2」は「2乗」を表します)
いきなりグラフを書く前に、ちょっとだけ図形を予想してみましょう。
・全体が2乗のグラフなので、図は全て「y = 0」より上に収まるはず。
・sin xは「x = 0, π, 2π, 3π…」でx軸と交わるので、
2乗してもこの周期で0と接する関数になるはず。
これを踏まえて、グラフを見てみましょう
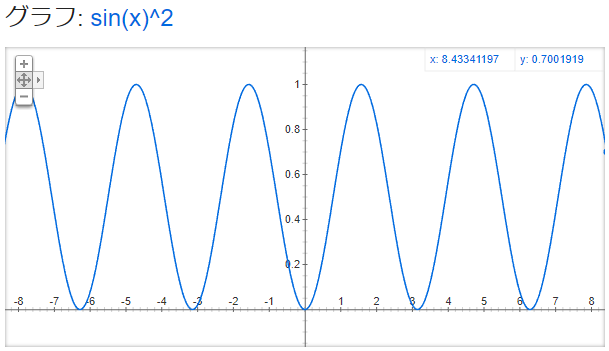
大体予想と合っていたでしょうか。
何となくこれも正弦波に形が似ていませんか?
このグラフも実は「正弦波」(の拡大と平行移動)で表せます。
今度の証明は各自で試してみて下さい。
ヒントは、コサインの加法定理をa = b =xと代入して用いることです。
いわゆる「倍角公式」とも呼ばれる式ですが、加法定理だけ覚えていれば導けます。
干渉を図示してみる
物理では、音や光で「干渉」という現象を扱います。
簡単に言えば「波が重なり合う現象」のこと。
上でやった「y = sin x + cos x」も一種の干渉と言えるでしょう。
この項では、わかりやすくするためにコサインを使わずに話を進めます。
また、ここからのグラフでは、
赤と黄が干渉前の波、
青が干渉の結果生まれる波
として描画することにします。
まず、わかりやすい干渉の例として、
「同じ周波数の波」の干渉を紹介しましょう。
y = 3 sin x + 2 sin (x - π), y = 3 sin x, y = 2 sin (x - π)
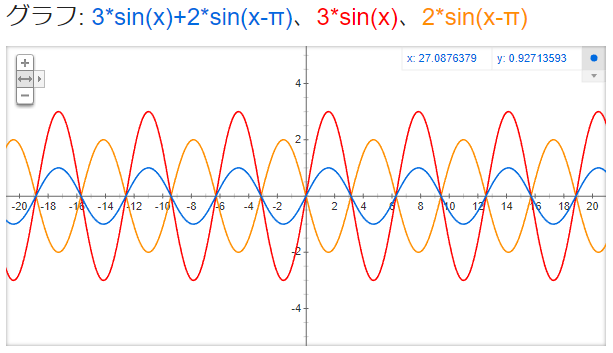
それから、強め合う波があります。
y = 3 sin x + 2 sin x, y = 3 sin x, y = 2 sin x
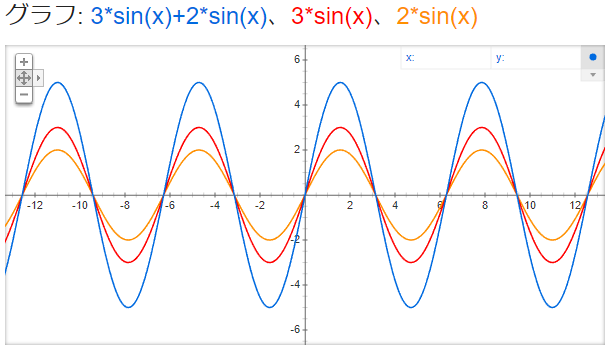
中途半端なズレ方の干渉だと、先程の「y = sin x + cos x」のように、
「同じ周波数で、位相と振幅が異なる波」が生まれます。
今度は「少しだけ周波数の違う波」を干渉させてみましょう。
y = sin x + sin (1.1x), y = sin x, y = sin (1.1x)
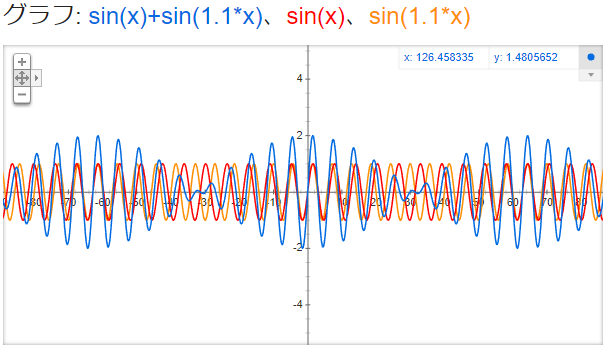
黄の波が赤の波よりほんのチョット(1割だけ)波長が短いです。
干渉によって生まれた青のグラフがどうなっているか、よく見て下さい。
見づらい黄と赤を消してみるとこんな感じ
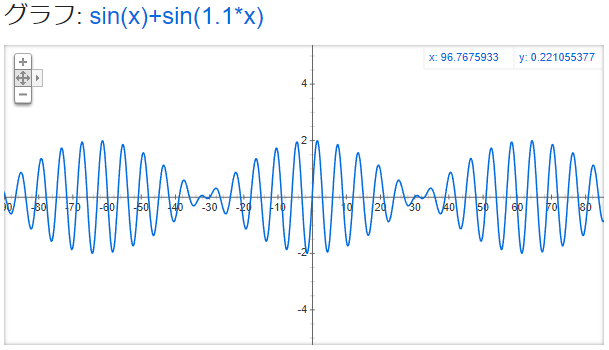
何が起こっているかお分かりでしょうか。
三色グラフで、今度は拡大してみましょう
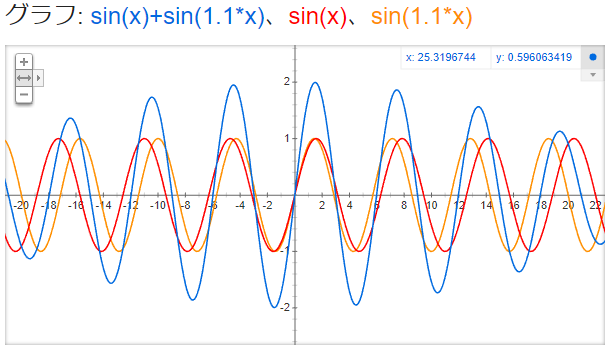
青のグラフが膨らんでいる所を見ると、赤と黄が重なっています。
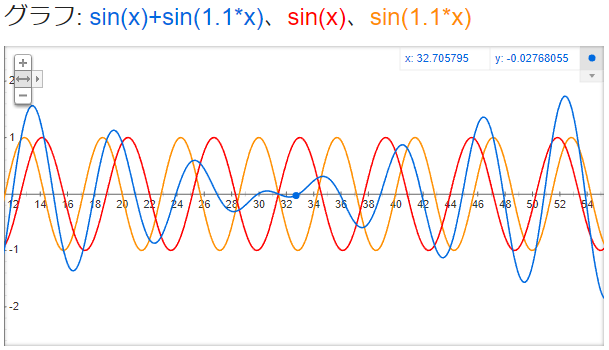
小さくなっている所を見ると、赤と黄が上下逆の動きをしています。
この項の冒頭に挙げた干渉の例では、波長はぴったり一致していたので、位相は同じ位置関係を保ったままでした。しかし、こちらのグラフでは波長が微妙にピッタリではないので、「弱め合う位相」と「強め合う位相」が交互にやってくることになります。
この「交互」のペースは、波長をどれくらいずらしたかに依存します。さっきの
y = sin x + sin (1.1x), y = sin x, y = sin (1.1x)
この式では、元の波長の1割のズレを作ったので、元の「y = sin x」の波が10回山を作るたびに最強点(最弱点)がやってくるわけです。
では次に、「50回ごとに強まる(弱まる)」ような波を考えてみましょう。
邪魔なので今度は最初から赤と黄色を消します。
y = sin x + sin (1.02x)
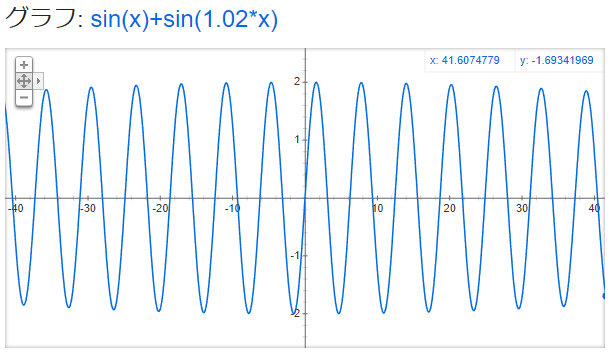
↑近くで見るとこんな感じ
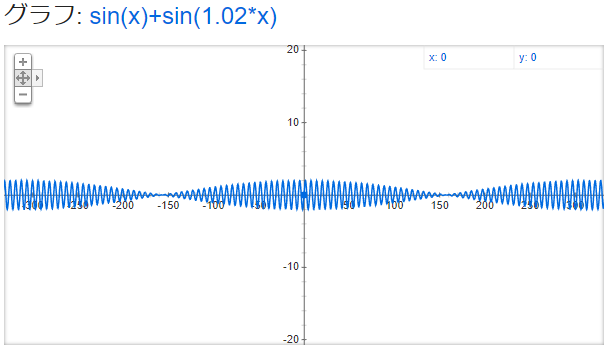
↑遠くで見るとこんな感じ
どうしてこんな形になるのでしょうか。
数式でこれを理解してみましょう。
y = sin x + sin (1.02x) ……②
ここでまた登場するのは最初の加法定理、つまり「シンコスたすコスシン」です
天下り的ですが、こういう2つの式を使って式②を作ることを考えましょう
sin(1.01x + 0.01x) = (sin 1.01x)(cos 0.01x) + (cos 1.01x)(sin 0.01x) sin(1.01x - 0.01x) = (sin 1.01x)(cos 0.01x) - (cos 1.01x)(sin 0.01x)
お分かりですね? 上の式と下の式を足します。
そうすると一番右の部分が消えるんですね。ガチャコンっと。
sin(1.01x + 0.01x) = (sin 1.01x) (cos 0.01x) + sin(1.01x - 0.01x) + (sin 1.01x) (cos 0.01x)
これを整理すると
sin(1.02x) + sin(x) = 2 (cos 0.01x)(sin 1.01x)
おっと、右辺にsinとcosの積が出てきました。
これはどう解釈したらいいのでしょう。
ここで一旦、cos 0.01xを2と一緒にまとめて、定数のようにみなしてみましょう。
つまりこう。
sin(1.02x) + sin(x) = 2 (cos 0.01x)(sin 1.01x) = (2 cos 0.01x) sin 1.01x
そうすると、これは「振幅付きの正弦波」の式とみなせることになります。
しかし実際にはcos 0.01xは定数ではなく、「角運動が非常にゆっくりな正弦波」なので、「めちゃくちゃゆっくりだけど増減する係数」ということになります。
y = 2cos 0.01 xをさっきのグラフに重ねてみると一目瞭然です。
y = sin x + sin (1.02x), y = 2cos 0.01 x
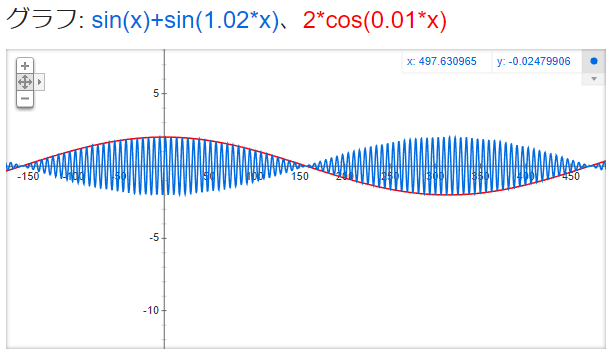
赤グラフのy = 2cos 0.01 xがy = sin x + sin (1.02x)の振幅を定める「外枠」のようになっていることがよく分かります。
この赤線の「ゆったりした消長」は、音であれば「うなり」と呼ばれます。
また、実はラジオ放送のAM(amplitude modulation)というやつもこの図と絡んでくるのですが……そっちの話に踏み込むと脱線が長いので各自調べて下さい。
今やった式変形は、「サインの足し算」を「『速く変化するサイン』と『遅く変化するコサイン』の掛け算」として解釈したことになります。
一般に「サイン、コサインの足し算」は「サイン、コサインの掛け算」に変換出来ます。そして、その逆も成り立ちます。
これらは、いわゆる「積和公式(和積公式)」を逆の視点から見たことになります。
https://mathtrain.jp/sekiwa
これらの公式は単なる「式」ではなく、具体的に現象と対応しているわけですね。
なお、「積和“公式”」と銘打っていますが、これも加法定理を足し引きして作れる定理なので、わざわざ覚えるほどのことはありません。
高校生は「倍角公式・半角公式」も「和積公式・積和公式」も、「加法定理からの作り方」で覚えれば十分でしょう。
記事が長くなってしまったので今回は一旦ここまで。
次回はこの三角関数が「音楽」にも役立つことを、実例で紹介しようと思います。
なお、三角関数の応用である「フーリエ変換」については、めるる氏が数学の「直交分解」という概念からアプローチして記事を書いています。
本記事の内容が易しすぎると感じた方は是非こちらにチャレンジしてみて下さい。
★ひとことまとめ
☆このトピックにオススメの本
数学ガールの秘密ノート/丸い三角関数
SBクリエイティブ, 2014/4/24
高校数学の学び直しとして定評のあるシリーズ。
会話形式で躓きやすいところがよくフォローされていたり、過程が丁寧に式で記載されているので、独学者に優しいです。
渋谷道雄(著), 晴瀬ひろき(作画), トレンド・プロ(制作):
マンガでわかるフーリエ解析
オーム社, 2016/5/20
「フーリエ解析」は音などの波を三角関数で解析する手法。
こちらは、そのエッセンスだけを漫画でサクッと概観できる一冊。
数式が少ないので、きちんと理解するにはやや物足りないですが、「三角関数でこんなことが出来るようになる」というイメージを持つには十分な内容です。
数学読本〈2〉
簡単な関数/平面図形と式/指数関数・対数関数/三角関数
岩波書店, 1989/12/18
高校数学をガチで理系高校生レベルまで独学するならこの一冊。
「読本」と言いつつ数式に妥協は無く、章末ごとに例題も付いてます。確かな理解を得て進みたい独学者にはこれでしょう。
難点は現在ではなかなか入手しにくいことですが……
参考文献
Webサイト
『高校数学の美しい物語』https://mathtrain.jp/
特に以下の3つの頁は本稿を参照する上で有用
https://mathtrain.jp/kahouteiri
https://mathtrain.jp/trig_basic
https://mathtrain.jp/sekiwa
この記事を書いた人
狐太郎
最新記事 by 狐太郎 (全て見る)
- AIサービスを活用した英文メール高速作成術 - 2023年3月28日
- 大学生・院生に便利なAIウェブサービスまとめ【2023年2月版】 - 2023年2月22日
- 「読書強者」が「速読」に価値を見出さない理由【隙間リサーチ】 - 2022年9月23日







