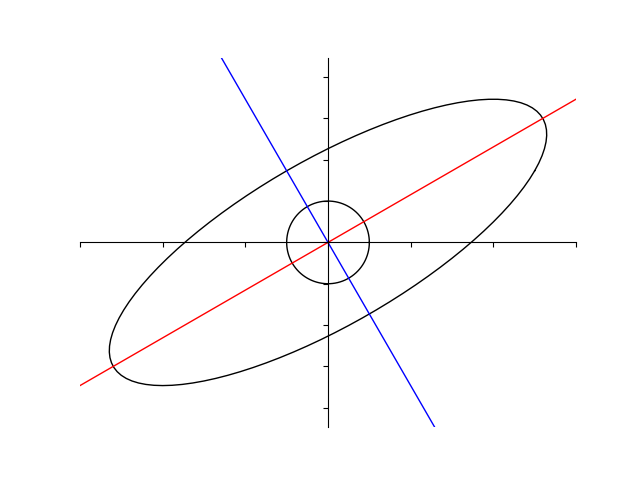
前回は行列は固有ベクトルの向きを変えないということを説明しました。
今回も引き続き、対称行列
$$A=\begin{pmatrix} 5 &\sqrt{3} \\ \sqrt{3} & 3\end{pmatrix}$$
を用いて、行列の固有値について解説をしていきます。
前回は行列は正方形を平行四辺形に写すものとして説明しましたが、今回は半径 \(1 \) の円(単位円)を写してみましょう。
行列 \(A\) による単位円の像は楕円形をしています。
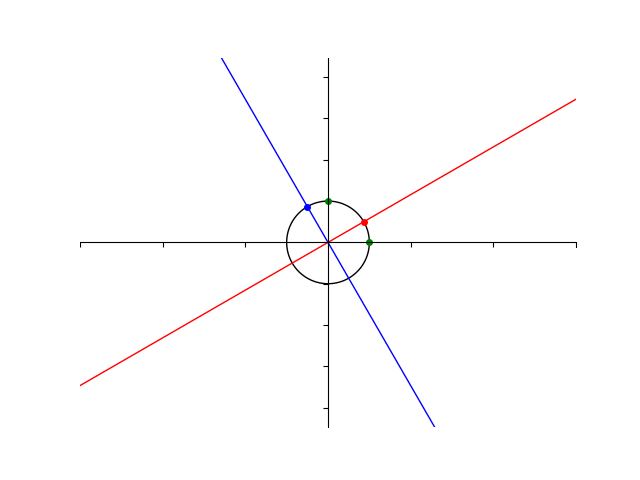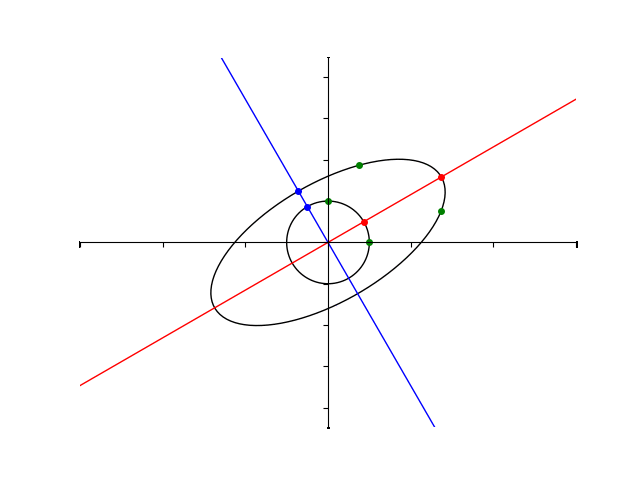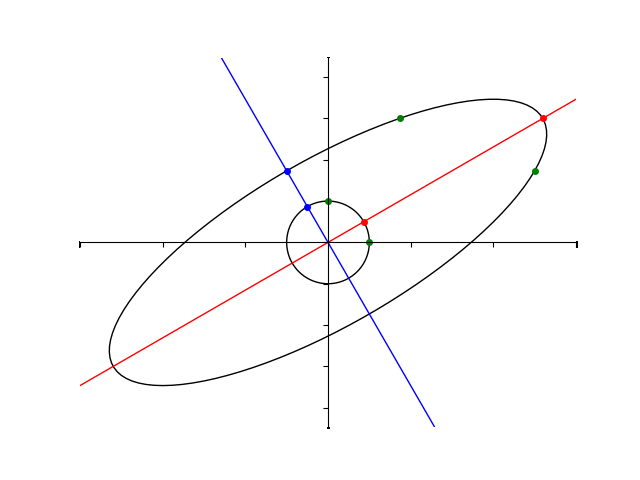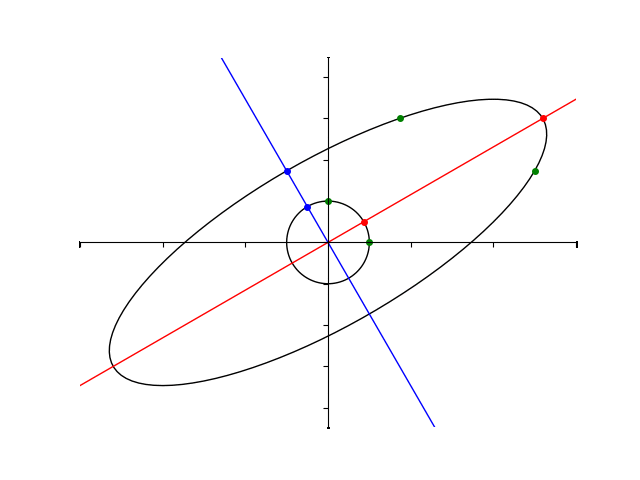
楕円の長軸、短軸がそれぞれ固有ベクトルと同じ向きを向いていそうなのがわかりますね。
これは偶然でしょうか?あるいは、たまたまそう見えるだけで、本当にそうなっているでしょうか?まずは計算して確かめてみます。
1. 楕円の長径、短径を求めてみよう
単位円上の点 \(x\) の座標は \( 0\le \theta < 2\pi \) を媒介変数として、
$$x = \begin{pmatrix} \cos{\theta}\\ \sin{\theta} \end{pmatrix}$$
と表せます。これを行列 \( A\) に作用させると、
$$ \begin{align}
Ax &= \begin{pmatrix} 5 &\sqrt{3} \\ \sqrt{3} & 3\end{pmatrix}
\begin{pmatrix} \cos{\theta}\\ \sin{\theta} \end{pmatrix}\\
&= \begin{pmatrix} 5\cos{\theta} +\sqrt{3}\sin{\theta}\\ \sqrt{3}\cos{\theta} +3\sin{\theta} \end{pmatrix}
\end{align} $$
となります。楕円の長径、短径の大きさを求めたいので、 \( |Ax|\) の最大値と最小値を求める問題と言うことが分かります。
\( |Ax| \) の最大・最小を取るのは \( |Ax|^2 \) が最大・最小になるときなので、
$$ \begin{align}
|Ax|^2
&= (5\cos{\theta} +\sqrt{3}\sin{\theta})^2+( \sqrt{3}\cos{\theta} +3\sin{\theta} )^2\\
&= 25\cos^2{\theta} +10\sqrt{3}\cos\theta\sin\theta+3\sin^2\theta\\
&\quad + 3\cos^2{\theta} +6\sqrt{3}\cos\theta\sin\theta+9\sin^2\theta\\
&= 28\cos^2{\theta} +16\sqrt{3}\cos\theta\sin\theta+12\sin^2\theta
\end{align} $$
の最大値と最小値を調べればよいことが分かります。
高校生の頃を思い出して、次の問題を考えてみましょう。
半角の公式 \(\cos^2\theta =\frac{1+\cos{2\theta}}{2}、\sin^2\theta=\frac{1-\cos{2\theta}}{2}\) および倍角の公式より \(\cos\theta\sin\theta=\frac{1}{2}\sin{2\theta}\) をそれぞれ代入すると、
\begin{align*} f(\theta)&=8\sqrt{3}\sin{2\theta}+8\cos{2\theta}+20\\ &=16\sin{\left(2\theta+\dfrac{\pi}{6}\right)}+20 \end{align*}
ここで最後の変形には三角関数の合成公式を用いました。
\(\frac{\pi}{6}\leq 2\theta+\frac{\pi}{6}< \frac{13\pi}{6}\) により、
最大値は \(2\theta+\frac{\pi}{6}=\frac{\pi}{2}\) すなわち \(\theta=\frac{\pi}{6}\) のときで、\(f\left(\frac{\pi}{6}\right)=36\)
最小値は \( 2\theta+\frac{\pi}{6}=\frac{3\pi}{2}\) すなわち \(\theta=\frac{2}{3}\pi\) のときで、\(f\left(\frac{2}{3}\pi\right)=4\)
上記の計算から、 \(|Ax|\) は \(x = \begin{pmatrix}\cos{\frac{\pi}{6}} \\ \sin{\frac{\pi}{6}}\end{pmatrix}=\begin{pmatrix}\frac{\sqrt{3}}{2} \\ \frac12\end{pmatrix}\) のときに最大値 \(6\) をとり、
\(x = \begin{pmatrix}\cos{\frac{2\pi}{3}} \\ \sin{\frac{2\pi}{3}}\end{pmatrix}=\begin{pmatrix}-\frac12 \\ \frac{\sqrt{3}}{2}\end{pmatrix}\) のときに最小値 \(2\) をとることがわかりました。
前回の記事では行列 \(A\) の固有値と固有ベクトルは、
$$ (\lambda,v)= \left(6,\begin{pmatrix}\frac{\sqrt{3}}{2}\\ \frac12\end{pmatrix} \right), \,\left(2,\begin{pmatrix}\frac12 \\-\frac{\sqrt{3}}{2}\end{pmatrix} \right)$$
と得られていましたから、楕円の長軸、短軸がそれぞれ固有ベクトルと同じ向きをしており、さらにその長さは固有値に対応しているということがわかります。
下がそのときの様子を表す gif です。水色のベクトルの長さは、常に固有値の下限と上限である 2 と 6 の間の値をとることが分かるかと思います。

でも、たまたま \(A\) という行列がそういう性質を満たしているだけで、それ以外の行列もそうなっているとは限らないかもしれませんよね?
どんなときにこんな性質が成り立つんでしょうか?数学を使って考えていきましょう。
2. 内積とレイリー商
2つのベクトル \( x = \begin{pmatrix}x_1\\x_2\end{pmatrix}\) と \( y = \begin{pmatrix}y_1\\y_2\end{pmatrix}\) に対して、その内積 \( (x,y)\)を
$$ (x,y) = x_1y_1+x_2y_2$$
と書き表します。この定義から、内積と距離の間には \((x,x) = |x|^2\) という関係があることがわかりますね。
(ところで、高校数学では内積をコサインを使って定義していました。その定義と同じものになっているか、各自確かめてみてください。)
また、行列 \(A\) に対するレイリー商 \( R_A\) を
$$R_A(x) = \frac{(x,Ax)}{(x,x)} \quad x\neq 0$$
により定めます。レイリー商に対しては、今回のメインテーマである次の定理(レイリーの原理)が成り立ちます。
$$\max_{x\neq 0}R_A(x)=\lambda_{max},\quad \min_{x\neq 0}R_A(x)=\lambda_{min}$$
が成り立つ。さらに固有値 \(\lambda_{max}\) に対応する固有ベクトルを \( v_{max}\)、固有値 \(\lambda_{min}\) に対応する固有ベクトルを \( v_{min}\) としたとき、
$$R_A(v_{max})= \lambda_{max},\quad R_A(v_{min})= \lambda_{min}$$
が成立する。
上の定理から、最大固有値と最小固有値はレイリー商の最大値と最小値となっていることがわかります。
これを使って、楕円の長軸、短軸との対応を考えてみます。一般の正方行列 \(A\) に対して、その転置行列を \(A^T\) と表すことにすると、 \( (Ax,y)= (x,A^T y)\) が成り立ちます。
特に対称行列に対しては、\(A=A^T\) により、
$$\begin{align}
|Ax|^2 &= (Ax,Ax)\\
&= (x,A^TAx)\\
&= (x,A^2x)
\end{align}$$
が成り立ちます。さらに \(A^2\) の固有ベクトルは \(A\) の固有ベクトルと一致しており、固有値は \(A\) の固有値の二乗になっていることから、
\(A^2\) に対して上で紹介したレイリーの原理を適応すると、この最大値が \(\lambda_{max}^2\) で最小値は \(\lambda_{min}^2\) ということがわかりますね。
ここでの計算には \(A\) の具体的な数字は一切使っていません。なので、一般の実対称行列に対しても、”拡大率”の最大値と最小値が最大固有値と最小固有値に対応していることがわかりました。
3. ミニマックス定理
さらに、固有値が沢山ある場合(つまり、行列が \(n\)次の実対称行列の場合)にもミニマックス定理と呼ばれる次の定理が知られています。
$$\lambda_k = \min_{U,dim(U)=k} \max_{x\in U\setminus\{0\}}R_A(x)$$
が成立する。
うーん、突然これは難しいですね。じっくり見てみましょう。\(n=2\) の場合に書き直すと、
$$\begin{align}
\lambda_2 &= \max_{x\neq 0}R_A(x)\\
\lambda_1 &= \min_{U,dim(U)=1}\max_{x\in U\setminus\{0\}}R_A(x)
\end{align}$$
と表せます。1つ目の式を良く見るとレイリーの原理と同じく、 \(\max_{x\neq 0}R_A(x)\) が行列 \(A\) の最大固有値であることを主張しています。
2つ目の式を眺めてみましょう。\(\min_{U,dim(U)=1}\cdots\) の部分は \(\cdots\) の部分を最小にする直線 \(U\) を求めます、ということです。
固有値 \(\lambda_2\) に対応する固有ベクトルが”拡大率が大きいもの”として既に得られているので、それとは直交する方向が選ばれることになります。
つまり、ミニマックス定理は、”最大固有値とは、(対称)行列によってもっとも大きくなるベクトルの拡大率である”、そして、”次に大きい固有値は、それまでに選ばれたベクトルとは直交するもののうち、もっとも大きくなるベクトルの拡大率である”…ということを表しているんですね。
最適化にもミニマックス定理と呼ばれる別の定理が知られている(むしろそちらのほうが有名かも?)ので、それとは区別するためにこの定理を「クーランのミニマックス定理」などと呼ぶことが多いです。
また、統計学における多変量解析では分散共分散行列という実対称行列を扱う場面があり、大きい固有値に対応する固有ベクトルは分散が大きい方向を表しているため、そのようなベクトルを主成分と呼んで解析することがあるようです。
4. おまけと次回予告
対称行列に限って考えれば、固有値と”拡大率”の間には美しい対応があることがわかりました。
一方で、対称ではない行列 \(B\) を考えましょう。例として、
$$B=\begin{pmatrix} 5 &\sqrt{3} \\ -\sqrt{3} & 1\end{pmatrix}$$
とします。単位円をこの行列で写すとやはり楕円が得られます。

ところが、行列 \(A\) の場合とは異なり固有ベクトルではないところで”拡大率”の最大化と最小化がおきています。
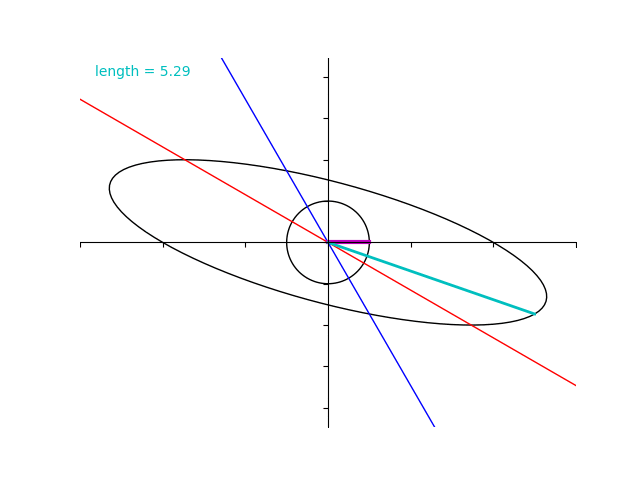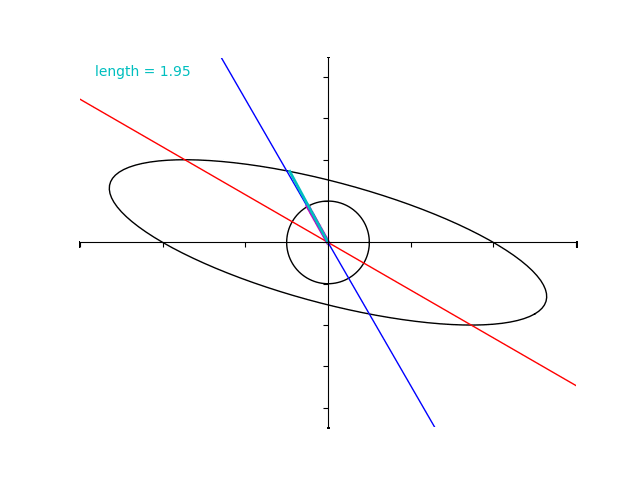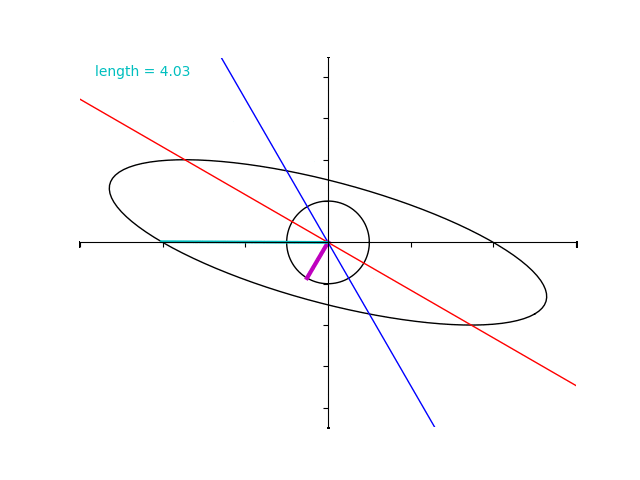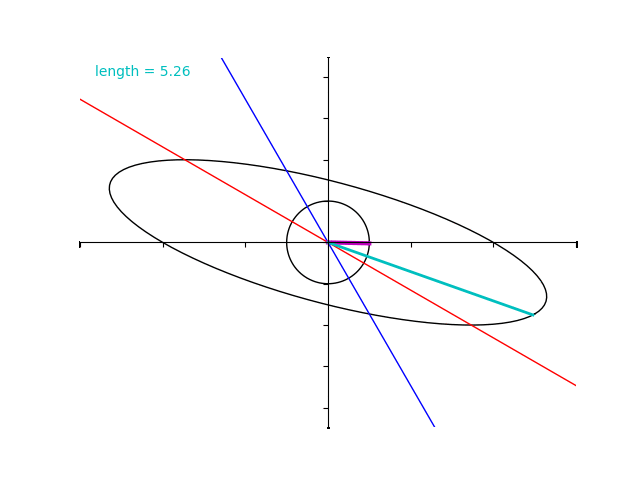
実際に、 \(B\) の固有値は 4 と 2 であるにもかかわらず水色のベクトルの大きさはそれよりも超過してしまっていますね。
このような対称ではない行列に対しては、上に述べたレイリーの原理は成り立ちません。
次回はこういった例に対して、特異値や特異ベクトルといった概念を使ってこの楕円への変形を説明をしていきます。
わかばめ
最新記事 by わかばめ (全て見る)
- 常微分方程式の解の一意性が成り立たない例についてざっくりと。 - 2018年9月2日
- フーリエ変換は自然現象を捉えるのに便利である - 2018年7月21日
- フーリエ変換とは無限次元空間の直交分解のひとつである - 2018年5月30日