前回の記事では、三角関数をグラフで視覚化してみました。
音階や和音の数学的関係についてはよく語られますが、音にはもっと素朴な「波の物理現象」としての面白さがまだまだ隠れています。
今回は、前回書ききれなかった「音の現象との対応」を紹介していきます。
なお、今回は「フリーソフトで誰でも自分のPCから実験できる」ものを目指しました。
http://efu.jp.net/soft/wg/wg.html
この「WaveGene」を使って遊びます。
必要な音源・画像は記事の中だけで完結することを目指しましたが、出来れば前回同様にちまちまと自分でパラメータをいじりながら読んでもらう方が嬉しいです。
理解も進んで楽しいと思うので。
Pythonのnotebookなんかが使えるともうちょっと気の利いたコトができると思うんですが、そこは他の人に譲ることにしましょう。

WaveGeneで正弦波を作る
自然界では「正弦波そのもの」の音を耳にする機会はまずありません。
聞いたことがあるとしても、電話機や、シンセサイザーのような電子楽器か、テレビやゲームに限るでしょう。
というわけで、まずは普通に「サイン波の音」を聴いてみましょう。
WeveGeneを起動するとこんな画面が出てきます。
次に、赤線を引いたところを同じ設定にして下さい。
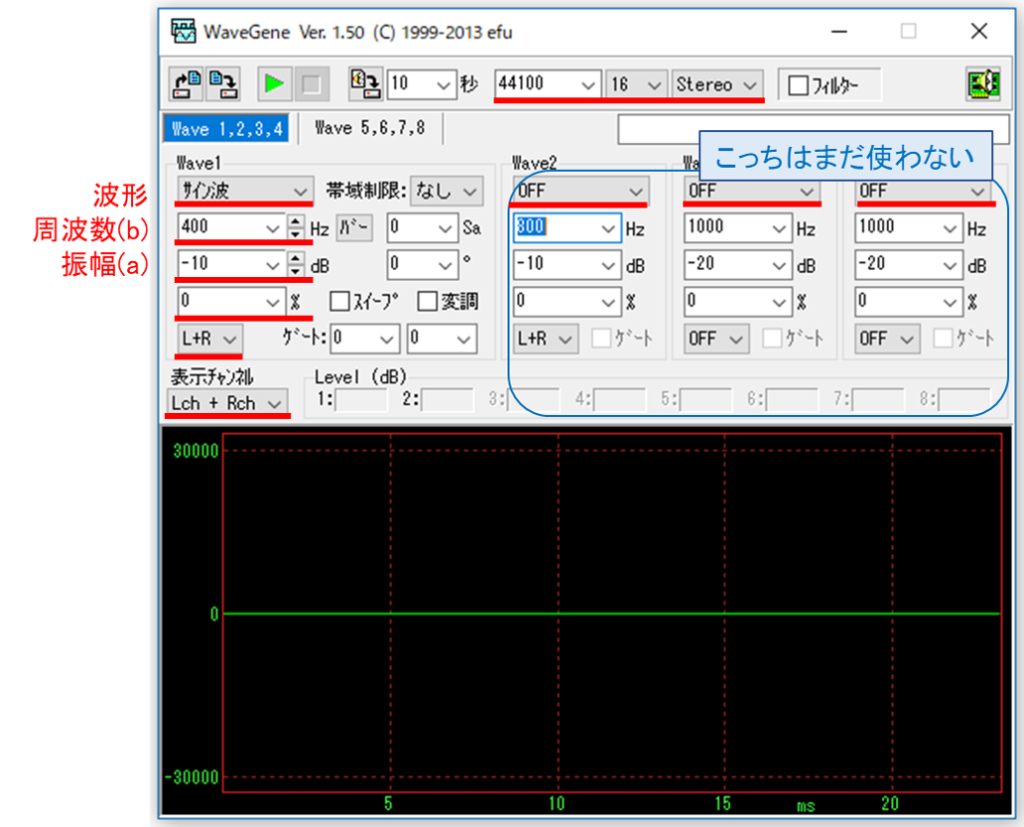
ソフトの各窓の意味と、数式的な対応を簡単に紹介しておきます。
前の記事で紹介した「周波数」は「音の高さ」に対応します。単位はHz(ヘルツ)。
「波の振幅」は「音の大きさ」になります。単位はdB[デシベル]。
振幅をa、周波数をb、時間をxとするなら、グラフは
y = a sin bx
と表せることになります。
では、さっきの設定で▶を押して再生してみましょう。 ※音量に注意
こんな音が出ます。
音が出ると同時に、下の窓に波の形が出てきましたね。
これからここにも注目していきましょう。
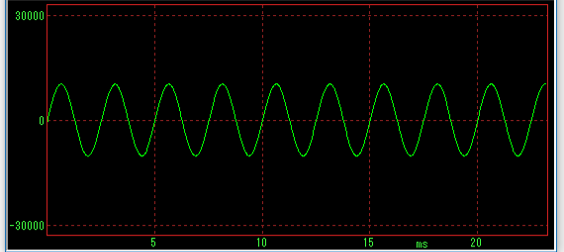
(下の窓はデフォルト設定では約20ミリ秒(つまり1秒の1/50)が表示されます)
この図形が前回Googleでいじり倒した「正弦波」であることは、パッと見て何となく納得してもらえるかと思います。
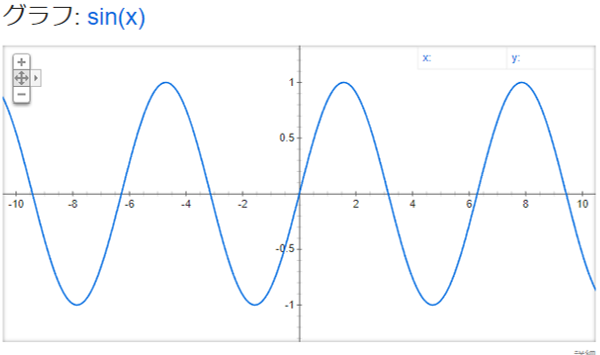
「正弦波は自然界ではまず聞けない」と言いましたが、
「フルートの高音部の波形が、強いて言うなら近い」と言う人もいます。
一応聴いてみましょうか。
2000Hzの正弦波はこんな感じです。ちょっとフルートのイメージが湧きます?
(多分あまり湧かないと思いますが……)
なお、数学だけだと軸のスケール感がつかめないので、周波数について補足します。
「Hz(ヘルツ)」は周波数の単位で、「1秒間にその数だけ振動する」ということです。
「100Hz→200Hz」に変えた時と「1000Hz→1100Hz」に変えた時の聴感上の変化を試してみると、「音の高さは対数的である」という意味がちょっと体感できます。
「1000Hz→1100Hz」だと「チョット上がる」、「100Hz→200Hz」だと「オクターブ上がる」というのが何となく分かるでしょうか。
参考までに、周波数と音の高さの目安になる値をいくつか紹介します。
20Hz……人間の可聴域下限
27.5Hz……ピアノ(88鍵)の最低音
82Hz……ギター(6弦)の最低音
100Hz~200Hz……一般的な男性の話し声
200Hz~300Hz……一般的な女性の話し声
1245Hz……ギター(6弦)の最高音
4186Hz……ピアノ(88鍵)の最高音
16000Hz~18000Hz……モスキート音
20000Hz……人間の可聴域上限
縦軸のdB(デジベル)は後々機会があれば触れますが、今回はスルーしてください。
干渉を観察しよう
使い方がわかったところで、前記事の最後で紹介した干渉を実演してみましょう。
今回は周波数を440Hzと442Hzに設定します。
2つの音を重ねるので、「Wave2」の「OFF」になっているプルダウンを「サイン波」に変えましょう。
設定は以下の通りです。(以降、同一設定部分は紫、変更部分は赤で示します)
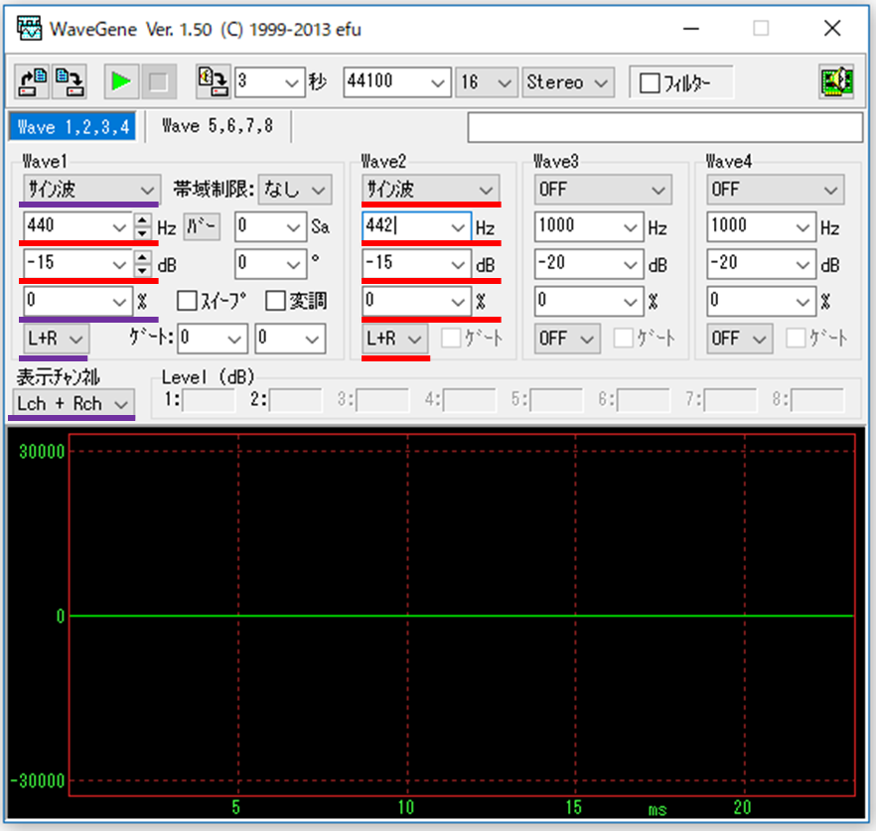
前の記事で言う「係数の cos0.01x の波」が感じ取れたでしょうか?
「ウヮンウヮン」って感じの成分です。
振幅が下の窓にリアルタイムに描画されて「振幅が増減する」のが分かるので、実際にソフトを動作させて眺めると面白いです。
また、「Wave2」のプルダウンを「OFF/サイン波」で音を流しながらぽちぽち切り替えてみると「うなり」が出たり消えたりするのが分かります。
「Wave2」の周波数を「440Hz」や「441Hz」に変えたりなんかも試して下さい。
周波数帯を変えてもう一回干渉を実験してみましょう。
今度は1000Hzと1002Hzです。

音の高さは違うものの、「うなりの周期」は「440Hzと442Hz」の時と同じになっているのが分かりますか?
「音程感覚」は対数的なのに、この「うなり」を作るにはどうして「比」ではなく「差」なのか。
「同じ周期のうなり」をつくるのに、「1000Hzと1020Hz」ではない理由は、前記事の式変形を見るとわかります。
y = sin x + sin (1.02x)
前回扱った↑この式の代わりに、
y = sin (bx) + sin ((b+2)x)
としてみましょう。
すると、前回と同じ手順で、これは以下のように変形できます。
①:sin((b+1)x + 2x) = sin bx cos 2x + cos bx sin 2x ②:sin((b+1)x - 2x) = sin bx cos 2x - cos bx sin 2x ① + ②:sin (bx) + sin ((b+2)x) = (2 cos 2x)(sin bx)
つまり、前回の記事で「うなりを作る係数」とみなした部分(2 cos 2x)は、「周波数b」が100だろうが1000だろうが関係なく、「2つの音の周波数の差」だけによって決まる、ということです。
この「うなり」は楽器を扱う人にとっては身近なものです。
「うなり」に注目すると、「1Hz単位での周波数のズレ」に気付くことができるので、チューニングの際に非常に重宝するのです。
調律師は音叉を鳴らして弦を調律することがありますが、「同じ音になっているかどうか」を判断するのに「うなりが無いかどうか」は重要なポイントになります。だから、同時に鳴らして「音を干渉させて聴く」必要があるのです。
「干渉」というのは、音波という波が、空気という媒質の中で重なり合って初めて生じる物理現象なので、「うなり」を聞く時にも「空気中で2つの音を混ぜる」ことが一つのコツになります。
(もっとも、WeveGeneは中で既に「干渉」がシミュレートされているので、空気振動になった時点から「うなり」は与えられていますが)
では「右耳は純粋な440Hz、左耳は純粋な442Hz」で左右のチャンネルから微妙に違う周波数を聞いてみたらどうなるでしょう。
理屈の上では、これなら「干渉」は起きないので「うなり」は聞こえないはずです。
次の音源はイヤホンかヘッドホンで聴いてみて下さい。
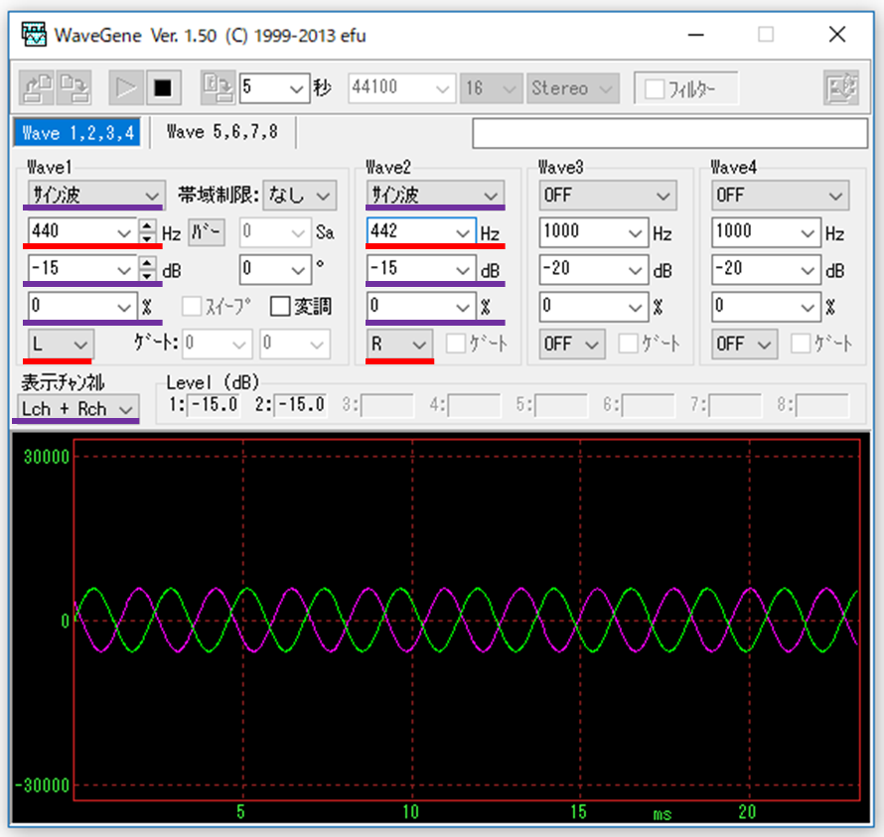
まず、イヤホンではどうでしょう。
「さっきほどはうなりが聞こえない」という人が多いと思います。
スピーカーで出力すると今回もはっきり「うなり」は聞こえるはずです。
しかし、もう一度よく聴いてみて下さい。人によってはイヤホンで聞いても、
「『うなり』らしきものを2Hzの周波数で感じる」人もいるのではないでしょうか。
これは、人間が「頭の中で波形を重ね合わせて聞いている」という証拠であるとともに、「耳から入った音情報は位相情報も保たれて脳に届いている」ということを示唆します。
ただ、高音域では聴神経の時点で位相情報が曖昧になると言われております。
実際、「ステレオ分離音源によるうなり」は「モノラルで重ね合わせたうなり」と違って、高音域では感じ取りにくくなります。
生物の話へと脱線してしまいました。物理の話に戻りましょう。
またモノラルの干渉を聞くので、Wave1,2ともL+Rに設定を戻します。
![]()
微妙に周波数をずらした音が「うなり」を感じさせることは分かりました。
これをもっとずらしていくとどうなるでしょう。
・440Hz+445Hz
Wave2の周波数を徐々に上げると「うなり」として感じられなくなってきます。
・440Hz+450Hz
・440Hz+470Hz
「揺れている音」とか「濁っている音」という感じがするんじゃないでしょうか。
あるいは、光線銃のオモチャの音を思い出す人もいるかも知れません。
・440Hz+530Hz
・440Hz+680Hz
更に離れると、2つの波はハッキリと分離して「2つの音」になってしまいます。
整数倍の音
先ほどの干渉では、「周波数をわずかにずらした音」は、「うなり」を伴いながらも一つの音に融合して聞こえることを示しました。
そして、「周波数が離れていくと、徐々に分離して聞こえる」ことも体感しましたね。
実は、これとは別に、「一体に溶け合って聞こえる波」があります。
それは、「整数倍の周波数の波」です。
今度は220Hzで正弦波をWave1に作りましょう。(もう設定は大丈夫ですよね?)
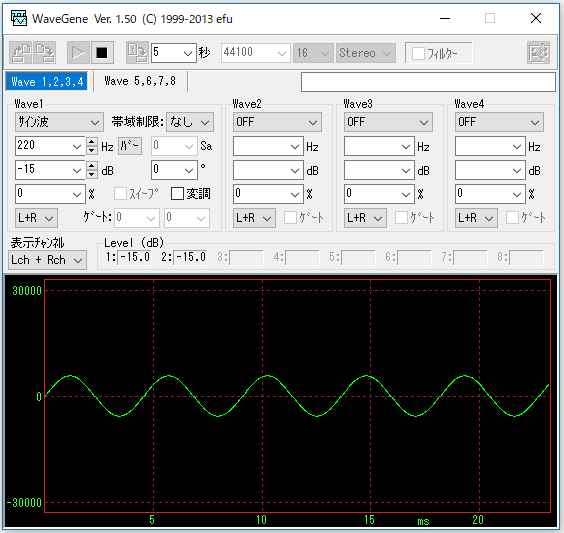
さっきより1オクターブ低い音。
そこにこんな組み合わせで音を重ねてみましょう。
・220Hz + 440Hz + 660Hz + 880Hz
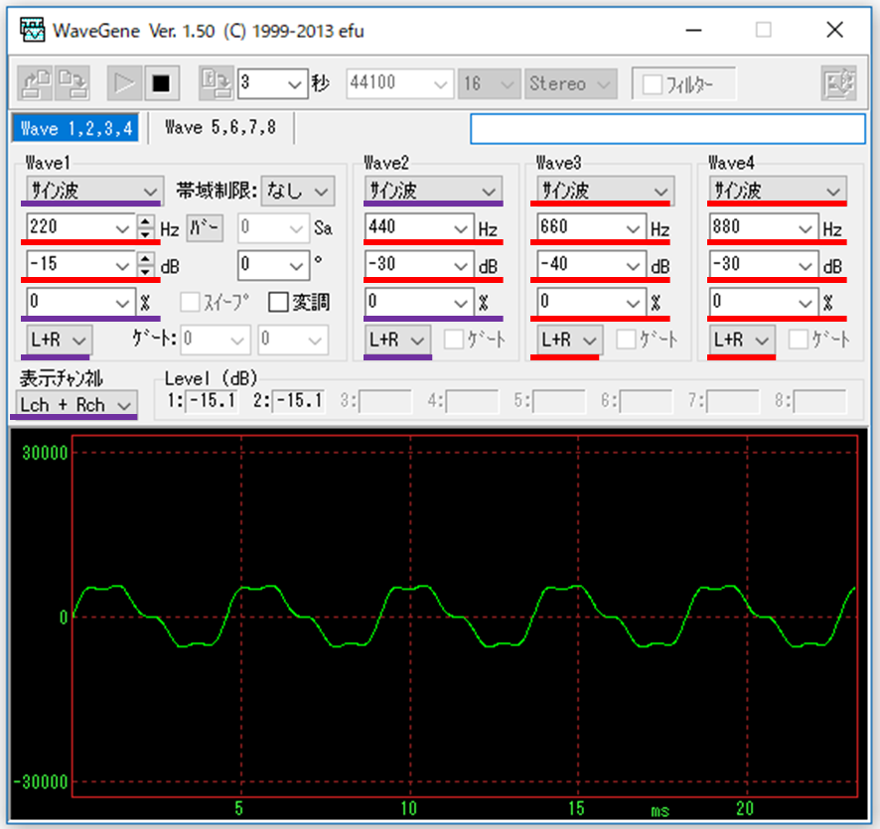
振幅を示す[dB]の窓に注目です。そして、下の波の形をよく見ておきましょう。
今度は振幅を示す[dB]の窓だけいじりますね。

音色が変わったのが分かるでしょうか?
次は周波数の構成も少し変えます。
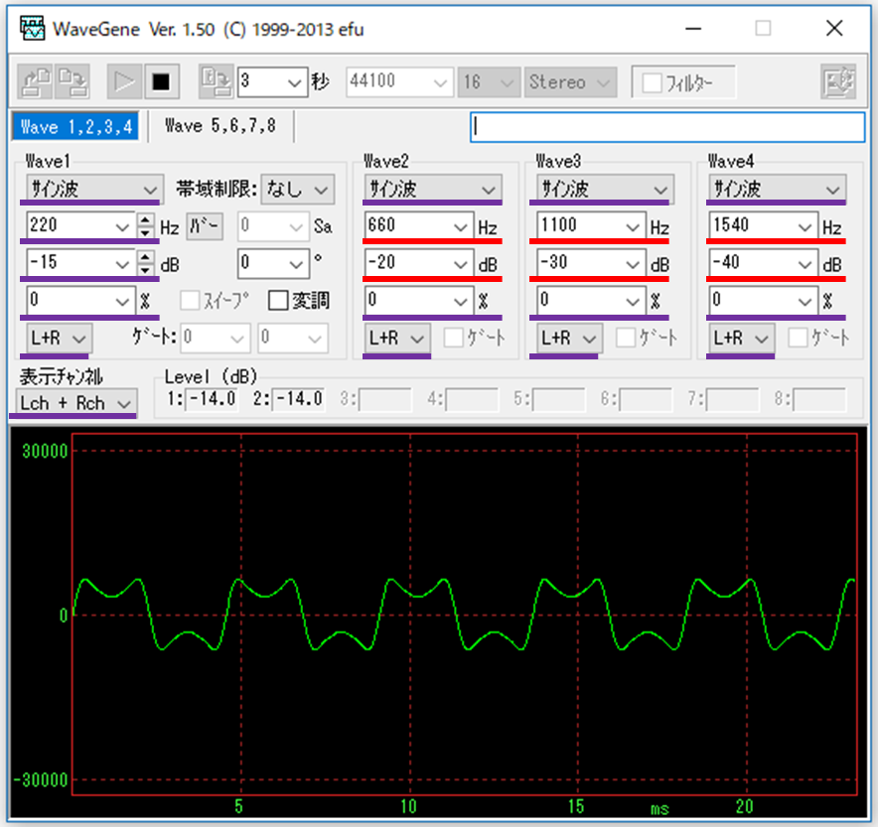
なんだか「木管楽器の音」っぽく感じて来ませんか?
記事も長くなってきたので簡潔に行きましょう。
楽器が「周波数220Hzの音」を出す際、波は「1/220秒の周期性」を持ちます。
一方で、(持続音における)「音の個性」とは「波形の個性」であります。
『同じ「周波数220の波」が、多様であるのは何故か』
その答えは『周波数220Hzでも波形が異なるから』です。
そしてその理由は、『周波数220nHzの波が加算されているから』です。
(ここでいう「220n」とは、「220の整数(n)倍の数」のことです)
これがどういう意味か、少し噛み砕いて解説します。
当たり前のことですが、「周波数220nの波」も、「1/220秒の周期性」を持ちます。
そして、ほとんどの楽器は、多かれ少なかれ「周波数220nの波」を含むのです。
(その理由は楽器の物理的構造に由来しますが、今回はこの説明は省略します。)
この「周波数220nの波」は「周期性は損なわずに波形だけ変化させる」わけです。
この時、基本の周期を作る波である周波数220Hzの音成分を「基底音」と呼び、
そこに加算されている周波数220nHzの音成分を「倍音」と呼びます。
さっきのWaveGeneの設定で、振幅を示す[dB]のところを自分でちょっとずつ変えてみると、「倍音の係数」が「音色」を変えている事実が確認できます。
これはご自分で試してみて下さい。
ところで、「倍音」の構成が「音色」を作っていることは分かりましたが、
この逆は言えるのでしょうか?
つまり、「どんな音色も倍音に分解して表現出来るのか?」
――という疑問が湧いてきます。
実はこれって結構深い問題に繋がっていたりします。
次はその辺まで接近できる記事を書きたいなーと思いつつ、本日はここまで。
また次回!(とは限らないけど)
★ひとことまとめ
☆このトピックにオススメの本
音のなんでも小事典
―脳が音を聴くしくみから超音波顕微鏡まで.
ブルーバックス, 1996/12/19
「音」を「科学」の観点からとことん解き明かす一冊。
コンパクトながら、扱っているトピックの幅広さは類書の中でもずば抜けています。
音楽や言語に興味のある方が本書を読めば、物理学や生物学に手を出したくなること間違いなしです。
楽器の科学
図解でわかる楽器のしくみと音のだし方.
サイエンス・アイ新書, 2013/4/16
整数倍の音の構成が「音色」を作ることは記事内で軽く紹介しました。
こちらの本では、様々な楽器を例に「どんな倍音構造になっているか」「それは何故か」を、物理的現象にまで踏み込んで解説しています。
「楽器を物理学的に理解したい人」にとって良い入門書です。
参考文献
書籍
日本音響学会(編): 音のなんでも小事典―脳が音を聴くしくみから超音波顕微鏡まで. ブルーバックス, 1996/12/19
柳田 益造(編): 楽器の科学 図解でわかる楽器のしくみと音のだし方. サイエンス・アイ新書, 2013/4/16
小方 厚: 音律と音階の科学 新装版 ドレミ…はどのように生まれたか. ブルーバックス, 2018/5/16
James O. Pickles: An Introduction to the Physiology of Hearing(Fourth edition). Brill Academic Pub, 2013/4/1
この記事を書いた人
狐太郎
最新記事 by 狐太郎 (全て見る)
- AIサービスを活用した英文メール高速作成術 - 2023年3月28日
- 大学生・院生に便利なAIウェブサービスまとめ【2023年2月版】 - 2023年2月22日
- 「読書強者」が「速読」に価値を見出さない理由【隙間リサーチ】 - 2022年9月23日






