二次の正方行列に対して、具体的な計算を通して特異値分解についての解説を試みます。
早速ですが、復習問題です。
2つの行列
$$A=\begin{pmatrix}5 &1\\1&5\end{pmatrix},\quad B=\begin{pmatrix}4 &2\sqrt{3}\\0&2\end{pmatrix}$$ に対して、次の各問いに答えよ。
(1) それぞれの固有値と固有ベクトルを求めよ。
(2) \(x = \begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix}\) に対して、\(|Ax|\) および \(|Bx|\) の最大値と最小値を求め、そのときの \(\theta\) の値を求めよ。
ヒント:(1) は行列の固有値と固有ベクトルの話を、(2)は対称行列とレイリー商、ミニマックス定理の話を参考にして解いてみましょう。
前回は、対称行列 \(A\) の固有値と、\(|Ax|\) の最大値・最小値には関係があることを明らかにしました。
下の gif においては、水色の線分の長さが \(4\) と \(6\) の間の値を取り続けており、固有ベクトルと一致する場合にその \(4\) と \(6\) の間の値をとることがわかります。
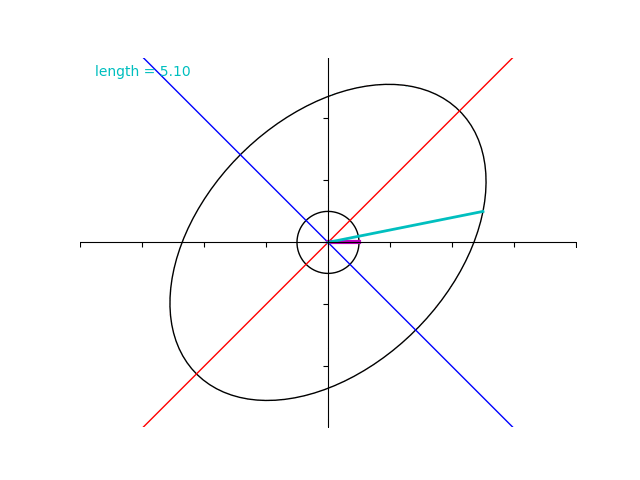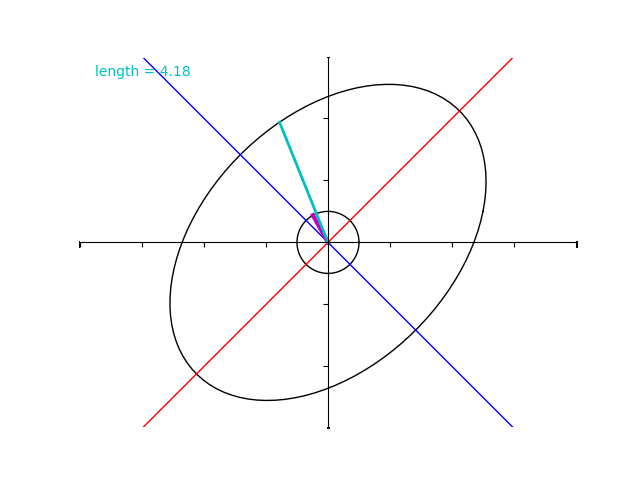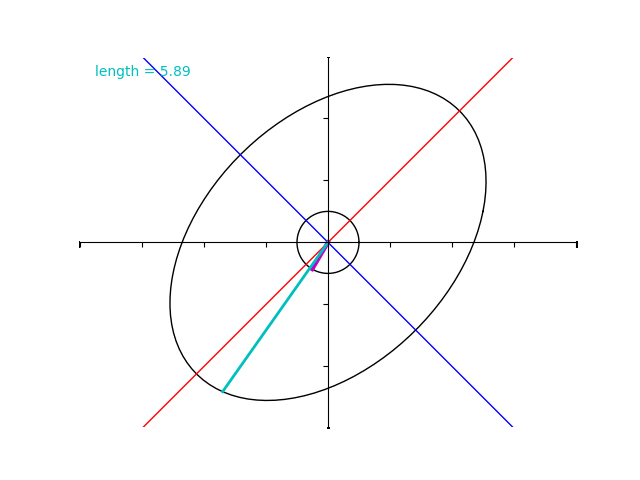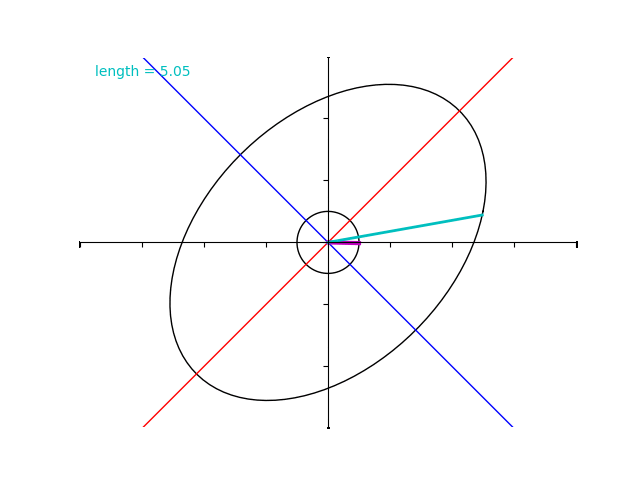
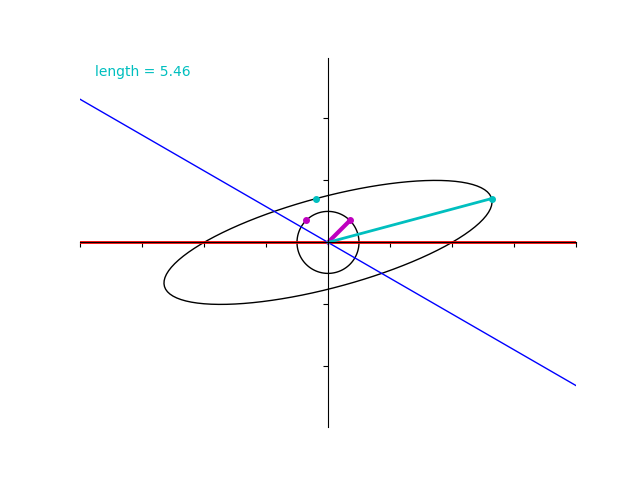
しかしながら、今みたように、対称ではない行列 \(B\) についてはその性質が成り立ちません。
単位円上の点と行列 \(B\) で写した点との対応を表す下の gif を見ると、固有値が \(2\) と \(4\) であるにもかかわらず水色のベクトルの長さはその範囲を超過しています。
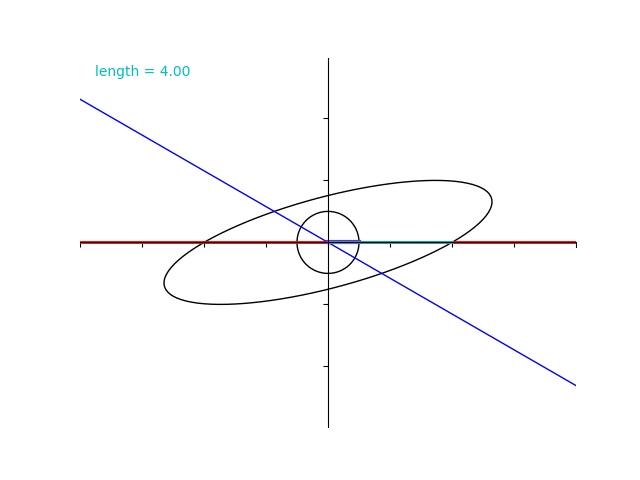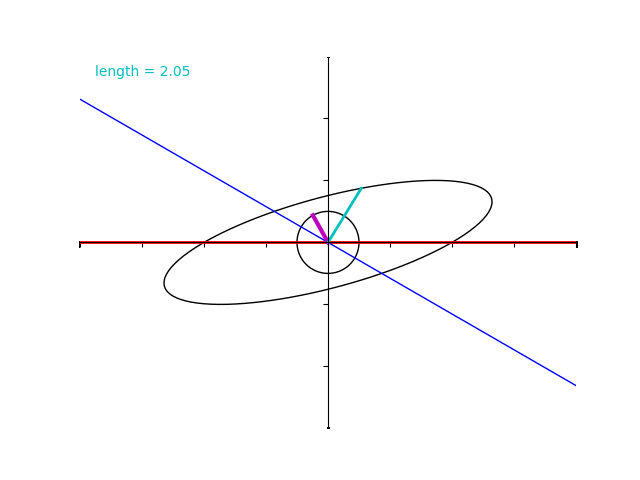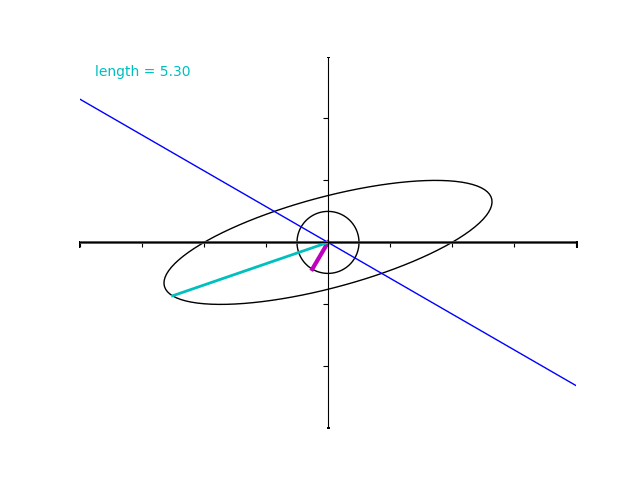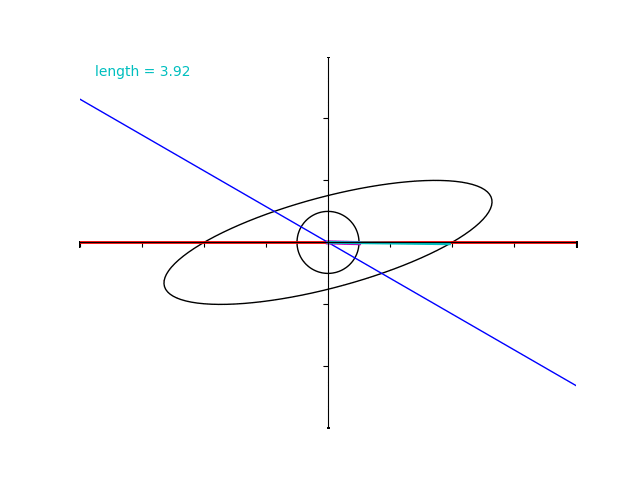
ゆっくり再生してみましょう。\(2\sqrt{3}+2= 5.46\dots\) と、\(2\sqrt{3}-2= 1.46\dots\) に注意します。
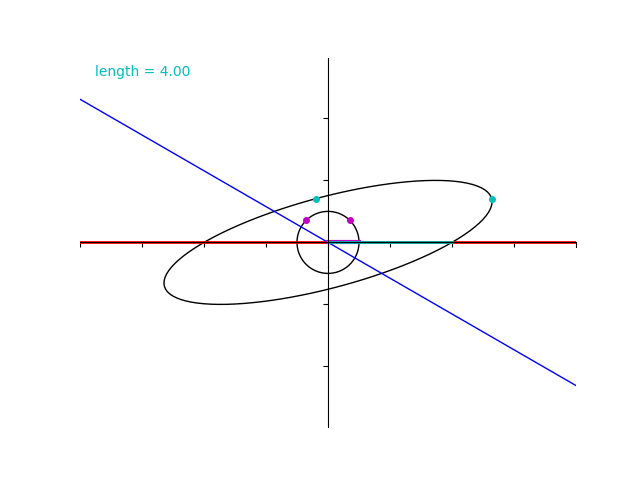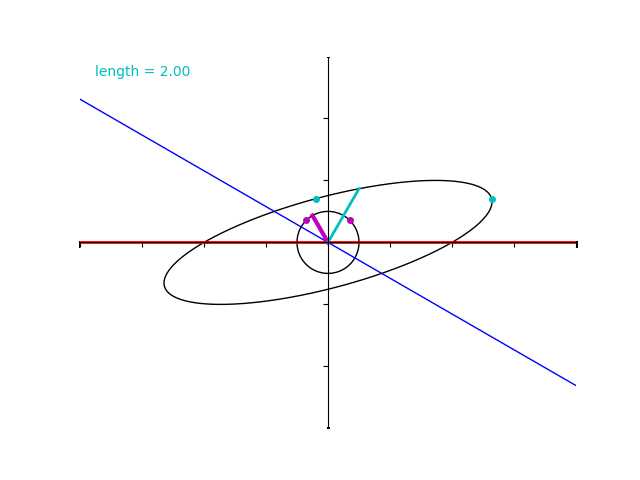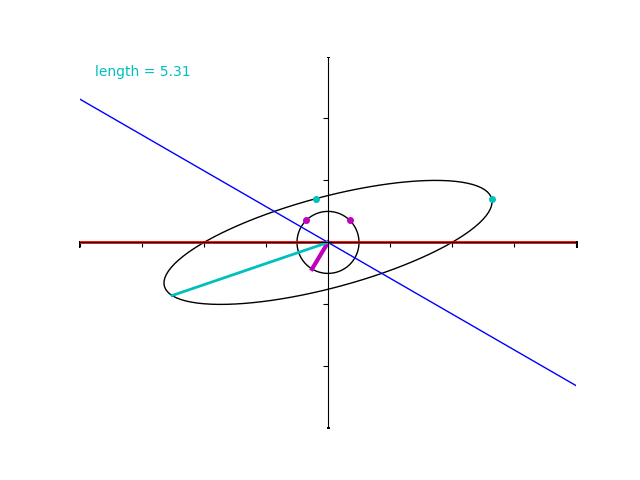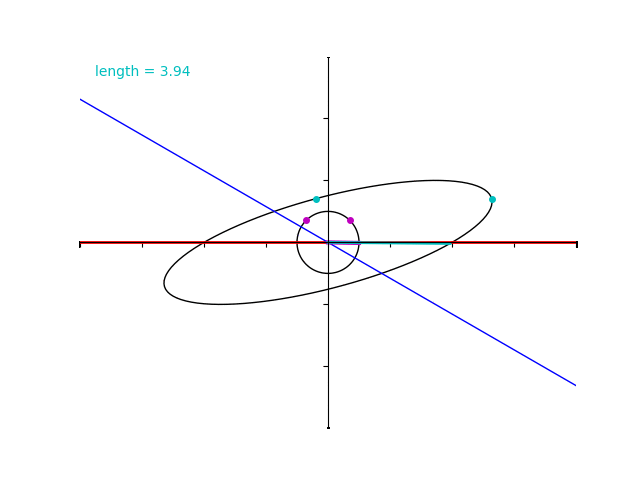
先ほどの演習問題で行ったとおり、紫色のベクトルの仰角が \(45^\circ\) のときに最大値 \(2\sqrt{3}+2 = 5.46\dots\) 、仰角が \(135^\circ\) のときに最小値 \(2\sqrt{3}-2= 1.46\dots\) なっていることが分かりますね。
では、今度は長径と短径の向きを求めてみましょう。次の問題を考えます。
行列 \(B=\begin{pmatrix}4 &2\sqrt{3}\\0&2\end{pmatrix}\) に対して、\(v_1=\begin{pmatrix}\cos\frac{\pi}{4}\\ \cos\frac{\pi}{4}\end{pmatrix}\)、\(v_2=\begin{pmatrix}\cos\frac{3\pi}{4}\\ \cos\frac{3\pi}{4}\end{pmatrix}\) とする。このとき
$$\frac{Bv_1}{|Bv_1|},\quad \frac{Bv_2}{|Bv_2|}$$
を求めよ。
まず、\(Bv_1\) を計算すると、
$$\begin{align}
Bv_1 &= \begin{pmatrix}4 &2\sqrt{3}\\0&2\end{pmatrix}\begin{pmatrix}\cos\frac{\pi}{4}\\ \cos\frac{\pi}{4}\end{pmatrix}\\
&= \begin{pmatrix}4\times \frac{\sqrt{2}}{2}+2\sqrt{3}\times\frac{\sqrt{2}}{2}\\
0\times\frac{\sqrt{2}}{2}+2\times\frac{\sqrt{2}}{2}\end{pmatrix}\\
&= \begin{pmatrix}\sqrt{2}(2+\sqrt{3})\\\sqrt{2}\end{pmatrix}\end{align}$$
一方で、\(|Bv_1|=2(\sqrt{3}+1)\) はさきほど求めたので、分数の有理化を思い出すと、
$$\begin{align}\frac{Bv_1}{|Bv_1|}
&= \begin{pmatrix}\frac{\sqrt{2}(2+\sqrt{3})}{2(\sqrt{3}+1)}\\\frac{\sqrt{2}}{2(\sqrt{3}+1)}\end{pmatrix}\\
&= \begin{pmatrix} \frac{\sqrt{2}(2+\sqrt{3})(\sqrt{3}-1)}{2(\sqrt{3}+1)(\sqrt{3}-1)}\\ \frac{\sqrt{2}(\sqrt{3}-1)}{2(\sqrt{3}+1)(\sqrt{3}-1)}\end{pmatrix}\\
&= \begin{pmatrix}\frac{\sqrt{6}+\sqrt{2}}{4}\\ \frac{\sqrt{6}-\sqrt{2}}{4}\end{pmatrix}
\end{align}$$
を得ます。半角の公式などを使うと、\(\cos\frac{\pi}{12}=\frac{\sqrt{6}+\sqrt{2}}{4}\)、\(\sin\frac{\pi}{12}=\frac{\sqrt{6}-\sqrt{2}}{4}\) がわかるので、
$$\frac{Bv_1}{|Bv_1|} = \begin{pmatrix}\cos\frac{\pi}{12}\\ \sin\frac{\pi}{12}\end{pmatrix}$$
を得ます。同様の計算により、
$$\frac{Bv_2}{|Bv_2|} = \begin{pmatrix}\cos\frac{7\pi}{12}\\ \sin\frac{7\pi}{12}\end{pmatrix}$$
を得ます。是非やってみてください。
以上のことから、
$$\sigma_1 = 2(\sqrt{3}+1)\quad\sigma_2 = 2(\sqrt{3}-1)\quad u_1=\begin{pmatrix}\cos\frac{\pi}{12}\\ \sin\frac{\pi}{12}\end{pmatrix}\quad u_2=\begin{pmatrix}\cos\frac{7\pi}{12}\\ \sin\frac{7\pi}{12}\end{pmatrix}$$
とおくことで、
$$Bv_i = \sigma_i u_i\quad i=1,2$$
が成立しています。このことを行列の表記で書きなおすと、
$$\begin{pmatrix} Bv_1&Bv_2\end{pmatrix}=\begin{pmatrix} \sigma_1 u_1&\sigma_2 u_2\end{pmatrix}$$
が成立しています。新たに二次の正方行列 \(V\) と \(U\) および \(\Sigma\) を
$$V=\begin{pmatrix} v_1&v_2\end{pmatrix}\quad U=\begin{pmatrix} u_1&u_2\end{pmatrix}\quad \Sigma=\begin{pmatrix}\sigma_1&0\\0&\sigma_2\end{pmatrix}$$
と書くことにすると、先ほどの式は
$$BV=U\Sigma$$
と書き表せます。さらに \(V\) の逆行列 \(V^{-1}\) を右から掛けると、
$$B=U\Sigma V^{-1}= U\Sigma V^T$$
が成り立ちます。ここで行列 \(V\) はユニタリ行列であることを用いました。
これがまさしく特異値分解です。行列 \(\Sigma\) の対角成分 \(\sigma\) を特異値、行列 \(U\) および \(V\) の列ベクトル \(u\) \(v\) をそれぞれ(特異値 \(\sigma\) に対応する)左特異ベクトル、右特異ベクトルと呼びます。
$$
\begin{pmatrix}4 & 2\sqrt{3}\\0&2\end{pmatrix}
=\begin{pmatrix}\cos{\frac{\pi}{12}} &\cos{\frac{7\pi}{12}}\\\sin{\frac{\pi}{12}} &\sin{\frac{7\pi}{12}}\end{pmatrix}
\begin{pmatrix}2\sqrt{3}+2 & 0\\0&2\sqrt{3}-2\end{pmatrix}
\begin{pmatrix}\cos{\frac{\pi}{4}} &\sin{\frac{\pi}{4}}\\ \cos{\frac{3\pi}{4}} &\sin{\frac{3\pi}{4}}\end{pmatrix}
$$
という数式が成り立ちます。実際に右辺を計算して、正しいことを確かめてみてください。
実は、ここまでの計算は必ずしも正方行列でなくても行うことができます。
次回はより一般的な行列に対する特異値分解の求め方について紹介した後、具体的な応用例について触れていきたいと思います。
わかばめ
最新記事 by わかばめ (全て見る)
- 常微分方程式の解の一意性が成り立たない例についてざっくりと。 - 2018年9月2日
- フーリエ変換は自然現象を捉えるのに便利である - 2018年7月21日
- フーリエ変換とは無限次元空間の直交分解のひとつである - 2018年5月30日