WAISのIQ(知能指数)について呟くと、こういうリアクションがよくあります。
曰く
「IQって年齢で割って出すものだよね?」
曰く
「過去最高の人は200以上あったらしいぞ」
これはWAISで採用されている「deviation IQ(分散IQ)」と、古典的な「ratio IQ(比率IQ)」とを混同している典型例です。
簡単に言えば上記への返答は「誤解です」のほぼ一言です。
心理学や統計学を学んでいない人では特にこの区別が付いていないことが多いようです。
Wikipediaの「知能指数」の「IQ(知能指数)の算出法」で解説されているにもかかわらず正しい認識が広まらないのは、あの記事でもやはり「よく分からない」と感じる人が多いからではないでしょうか。
今回は「偏差値」や「IQ」の算出を整理してみます。
予備知識無しで理解できる記事を目指してまとめてみました。

古典的なIQは「精神年齢÷実年齢」
おそらく多くの人が知っていて、同時に誤解しているのは
「知能テストのスコアを年齢で割ったものが知能指数」
という定義でしょう。
この定義は直感的で分かりやすいというのが利点です。
この算出法は現代から見れば古いのですが、まずはこの定義の誕生から見ていきます。
「IQ(Intelligent Quotient)」という発明品は、最初にBinet式の知能テストで使われました。
Binetのテストは子ども向けの知能テストであり、結果が「○歳相当の知的能力」という風にスコア化されていました。
これが「精神年齢 Mental Age」に当たります。
※日本では「精神 Mental」と言うと「意思力」や「人格」に近いニュアンスを帯びてしまいますが、英語ではもっと広く「認知機能」に近いニュアンスで使われています。
Binetの検査ではスコアが「精神年齢」で出てくるため、「この児童の精神年齢は実年齢に対して高いか低いか」に関心が生まれました。
このような需要から、TermanとSternによって、以下のような指標が提案されました。
IQ = (精神年齢/実年齢)×100
これが「IQ(知能指数)」という概念の始まりです。
この定義式は「精神年齢を実年齢で割って100を掛ける」ことを意味します。
つまり、実年齢5歳で精神年齢6歳ならIQ120。実年齢8歳で精神年齢6歳ならIQ75。
ということになりますね。
「年齢相応の精神年齢」ならば必ずIQは100になりますが、「100より高い子」「100より低い子」のIQが「100よりどのくらい高いか」「どのくらい低いか」は「他の年齢での精神発達の相場」によって決定されるわけです。
図で示すとこんな感じ。
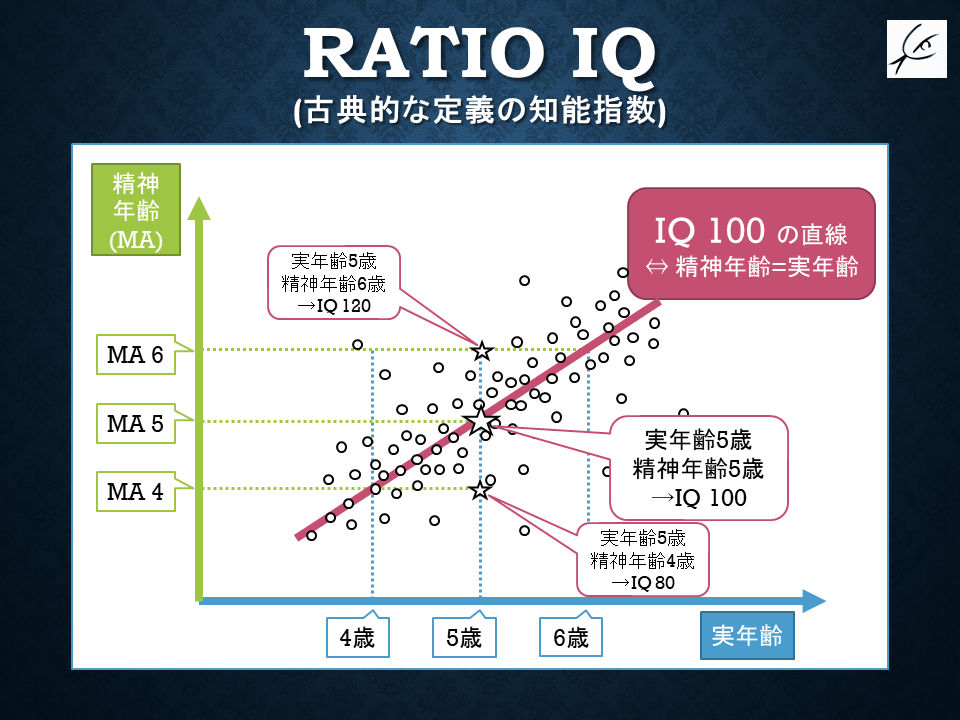
この方式で計算するIQは「計算が直感的」というメリットはあるのですが、指標としての安定性が弱いので現在はあまり使われていません。
日本で使われているBinet式検査でも、「精神年齢○歳△ヶ月」というスコアは必ず出てきますが、IQに換算したものを併記するかどうかはまちまちです。
Ratio IQの欠点は?
このratio IQは「この子は同年代の子と比べて賢いか賢くないか」の大雑把な目安としては悪くありませんでしたが、現代から見ると欠点や制約の多い指標でした。
ratio IQの欠点を具体的に見ていくと、次のdeviation IQが必要とされた経緯が良く分かると思います。
Ratio IQで「5歳の時に精神年齢7歳だった子が、10歳で測ったら精神年齢12歳だった」という状況を考えてみましょう。
この時、果たしてこの子の知能は下がったのでしょうか?
Ratio IQで見れば「IQは120から110になった」ことになりますが、精神年齢で見れば「常に実年齢より2歳分先取りした発達をしている」とも言えます。
「5歳の時点で予測される知能発達の相場から見て、10歳での知能は相応なのか、それより上昇や低下があるのか」という質問に、「ratio IQ」という指標のみでは何も答えられません。
子どもの知能発達は直線的な比例関係ではないからです。
更に大きな問題は、「ratio IQは子供の知能しか測れない」ということです。
知能テストで測られる能力のホトンド(言語知識に関するようなもの以外)は、基本的に20歳代で頭打ちになります。
では、40歳の人が20歳の平均と同じ点をとった時、IQは50ということになるのでしょうか?
更に極端な例ですが、80歳のお婆さんが知能テストで20歳の平均点を叩き出したらどうでしょう?
この人のIQは25?
いやいや、同年代内相対評価なら、この人は同年代の中でも相当に頭の回転が速い部類であるはずです。
IQという指標は「100を基準として、平均的な人より知能が高いか低いかを判定する」ために設定されていたわけですが、このように成人では正常に判定できなくなります。
「成人の場合は全て年齢を16歳とか18歳と決めて割り算する」という案もあります(そうやっているratio IQもあります)が、認知機能が下がり始める年齢に対応できないという点でやはりイマイチです。
また、子どもでも15歳くらいになると『クラスで一番頭のいい子』が『平均的な知能の大人が一生解けない問題』を解けるようになることがあるでしょう。
「この子の精神年齢は一体何歳なのか?」を設定できますか?
「精神年齢/実年齢」の分母は定まりますが、分子が定義できません。
Ratio IQは、「正常知能の発達が直線的な比例に近い」という想定の下でのみ意味を持つ指標です。
従って、「知能の向上が曲線であることを前提とする」場合や、「成人の知能を測る」場合や、「高すぎる知能を測る」場合には適さないということです。
これを踏まえて、WISCやWAISのIQの算出を見てみましょう。
Deviation IQはどう定義される?
Wechsler式で使われているIQは「deviation IQ」と呼ばれています。
簡単に言えば、「同年齢の子どもたちの点数を正規分布に乗せた時に、その分布のどこに位置するか」という換算で算出するものです。
この算出方法はratio IQとは全く違っています。
統計学をかじった人なら「平均100、SD 15で正規化を行う」と言うだけでも分かるかと思います。
以下では、統計学をやっていない人向けに、これをざっくり説明します。
あるテストを受けた人たちの得点パターンを図示した時、こんな感じの山になったとしましょう。

多くのテストはこういう風に、平均点付近が盛り上がった山形になります。
この形に近い有名な山の形で「正規分布」と言うものがあります。
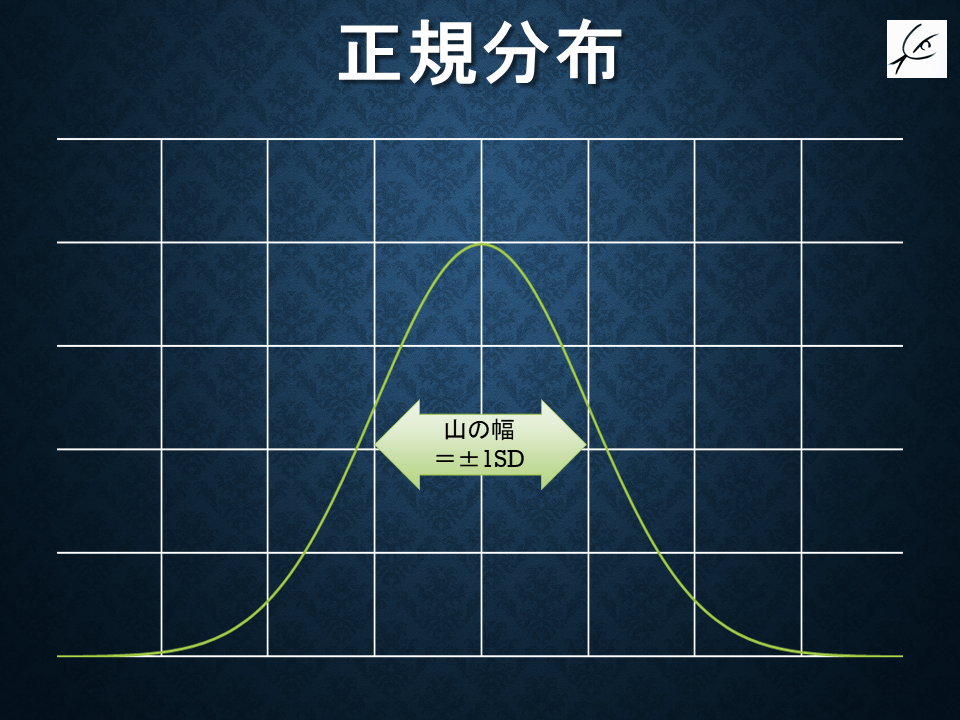
正規分布の山形は解析し尽くされているので、山が「正規分布」に近い形になっている場合には、これに当てはめると色んな事がわかります。
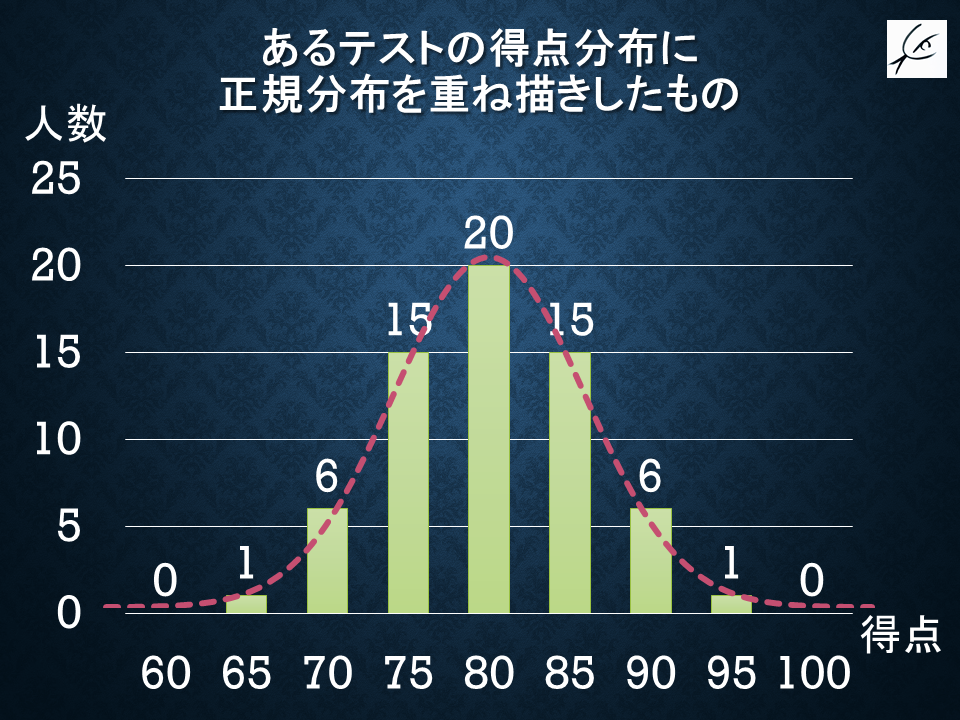
この「正規分布」に重ねるために、「山の横幅」に関する情報が必要になります。
この「山の横幅」を教えてくれる値を統計学では「SD(標準偏差standard deviation)」と呼びます。
SDの具体的な求め方が知りたい方はこちらのページやこんな本などを参考にしてみてください。
「このテストで何点の人は上位(下位)何パーセントに入るか」といったことが知りたい時、現実のテストの点数であれば「クラス全員のテストの点数」を参照したら分かりますが、例えばこれが「日本人全て」となってくると、「全員の点数を調べて答えを出す」ことはできません。
しかし、この「正規分布」という山に重ねる方法でなら、「上位(下位)何パーセント」というのが計算可能になります。
「山の真ん中」と「山の横幅」が分かれば、個別の受験者の点数に応じて、「君はこの山のここに相当するよ」ということが言えるのです。
これが「deviation IQ」に相当します。
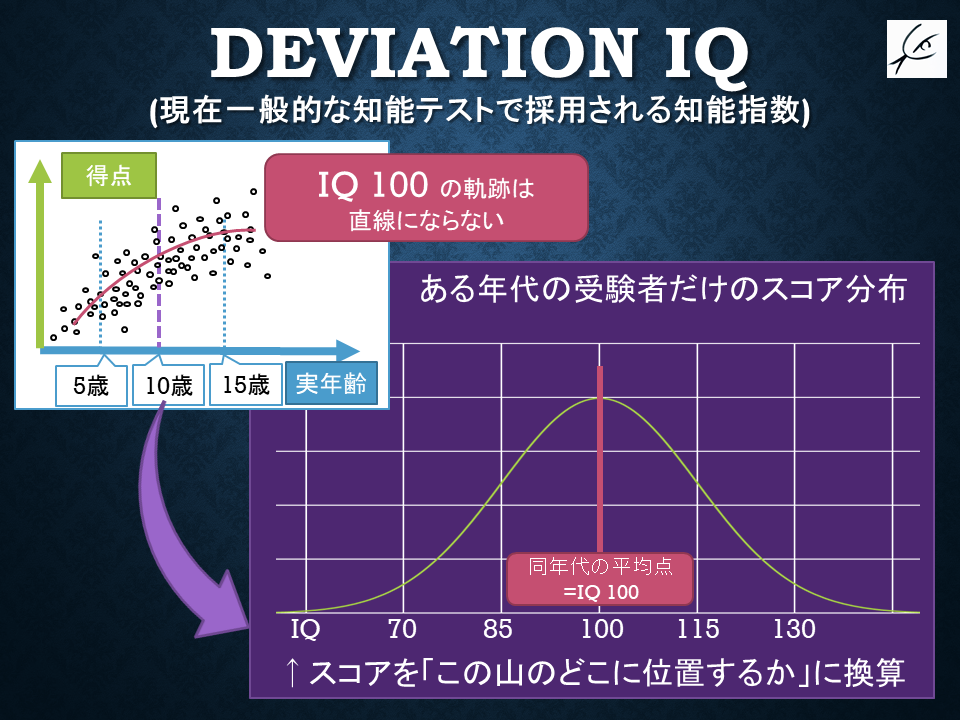
ここで、「知能テストを受けた人たちの得点パターンが正規分布になっている保証はあるのか?」と気になる方もいるかも知れません。
ここでは簡単に「Wechsler式の知能テストは、正規分布になるような問題セットを選んで作っている」と考えて頂いて構いません。実際、そういう統計的な調整をしています。
バランスの良いテストは正規分布になることが多いとは言われるものの、WAISのように統計的に上手く統制された検査でない限り、正規分布になることが一般に保証されるわけではありません。
以上を踏まえて、Wechsler式の知能テストで使われるdeviation IQを算出する式を見てみましょう
IQ = ((得点−平均点)/SD)×15 + 100
「平均的な子のIQ」は変わらず100になるよう設定されていますが、平均値より高い子・低い子に対して「どれくらい平均からはみ出しているか」を定量化するのに「SD(標準偏差)」を使っているわけです。
上の式を手続き的に解釈するなら、「得点が平均点と比べて何点高いかを計算して、それがSDの何倍に相当するか換算する。得点が平均点よりa×SD点高いとき、100+15aがその人の知能指数になる」と言ったところでしょうか。
この時、「平均点」と「SD」は、いずれも同じ年齢の人たちを対象に集計・算出します。
ちなみに、IQは「平均100、SD 15で正規化」したものですが、
「平均50、SD 10で正規化」すると学力偏差値の算出式になります。
つまり、こういうことですね。
学力偏差値 = ((得点−平均点)/SD)×10 + 50
あまり意味のない換算ではありますが、「学力偏差値をIQとして表したらどうなるか」を計算したければ、以下のようにも計算できます。
IQ’ = (学力偏差値-50)×1.5 + 100
何故そのように計算できるのかは省略しますが、興味のある方は考えてみてください。
もう一つの余談ですが、某高知能団体では入団条件を「上位2%の知能」としていますが、一方で「IQ140以上」と言っている人もいます。
これも種を明かせば「Wechsler式とは正規化が違う」というだけの話です。
彼らの算出法では「平均100、SD 24で正規化」しているようです。
「平均100、SD 24で正規化してIQ148」は「平均100、SD 15で正規化したIQ130」と同じです。
ただ、そもそもタスクの内訳が違うことや、高知能者しかいない団体がどうやって標準化したのか?といった問題は残りますが……。
話を戻します。
deviation IQで計算すると便利なのは、「deviation IQの値が△の人なら、同年代の上位□%に相当する」という関係が、何歳であっても一定に保たれることです。
deviation IQでは、「IQ135以上の人」は「同年代上位約1%の人」です。
これは対象集団が何歳であろうと、正規分布である限り揺るがない事実です。
IQの上がり・下がりは「同年代の中での相対的な立ち位置が上下した」ことを反映します。
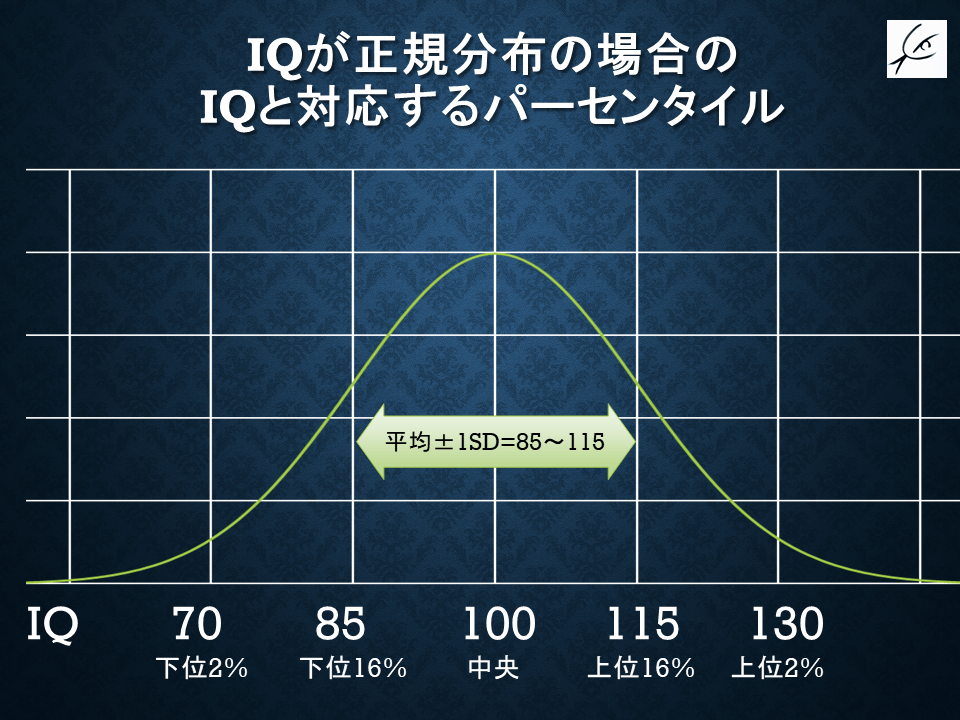
ここでは大雑把に±1SD,2SDの値しか書き込んでいませんが、
「あなたのIQ」を「上位(下位)何パーセント」へ変換したければ、
・あなたのIQが100から見てどれだけ大きいか小さいかを引き算で求める
・それがSDの何倍に相当するかを割り算で求める
・標準正規分布の中でそれが何パーセンタイルに相当するかを分布表から求める
という手順で出来ます。これも参考文献など併せてどうぞ。
繰り返しますが、「平均点」「SD」を計算するのに使うのは「同年代の得点分布」のみで済みます。
「その年齢の相場と比べて点数が高いか低いか」を算出するので、大人でも老人でも知能指数を定義できるようになるわけです。
上で挙げたratio IQの欠点がdeviation IQでは全て解決されていることがお分かりでしょうか。
このような利点から、現代ではdeviation IQが一般的に用いられています。
以上、古典的なratio IQと現在WAIS, WISCで使われるdeviation IQの違いについて、簡単にまとめてみました。
もう少しちゃんと理解したいという方は、下で紹介するような初歩的な統計の本で勉強することをおすすめします。
それほど難しい概念ではないので、初学者向けの統計の本を読めば1時間もかからずに納得できるかと思います。
おわりに
★ひとことまとめ
1. Ratio IQは「(精神年齢/実年齢)*100」で算出する
3. Deviation IQは「正規分布のどこに位置するか」で算出する
★参考文献
・書籍
1.Earl Hunt: Human Intelligence(2010, Cambridge University Press)
・Web
『統計Web』(https://bellcurve.jp/statistics/blog/15344.html)
小島 寛之:
完全独習 統計学入門.
ダイヤモンド社, 2006/9/28
今回登場した統計概念をちゃんと理解するならこのくらいの入門書が必要かなと思います。
分散・標準偏差、標準分布、パーセンタイルといった概念をちゃんと押さえるのに、最も敷居の低い本だと思います。
結城 浩:
数学ガールの秘密ノート
やさしい統計.
SBクリエイティブ, 2016/10/29
こちらも概ね上記の本と守備範囲は同じくらい。
高校数学が分かるくらいの人に良いかもしれない。
★この研究会について
以下の書籍の輪読会をインターネット上にて定期開催しています。
Earl Hunt: Human Intelligence(2010, Cambridge University Press)
本記事は輪読会の内容を元に、メンバーのトークも盛り込んでサマライズしたものです。
トピックや話の流れは上記のテキストを踏襲していますが、内容は再解釈の上で大幅に加筆や再編を加えています。
なお、研究会に参加をご希望の方はこちらの記事をご覧ください。
この記事を書いた人
狐太郎
最新記事 by 狐太郎 (全て見る)
- AIサービスを活用した英文メール高速作成術 - 2023年3月28日
- 大学生・院生に便利なAIウェブサービスまとめ【2023年2月版】 - 2023年2月22日
- 「読書強者」が「速読」に価値を見出さない理由【隙間リサーチ】 - 2022年9月23日