「IQテスト」と「大学入試」の基礎理論には共通する部分があります。
これは以前の記事でも指摘していますが、何故かと言えばIQテストは「頭脳の個人差を数値にして客観化する」という目的を突き詰めて作られているからです。
そう、「知能テスト Intelligence test」の理論には、センター試験のような大学入試のテストを考える上でも非常に有用な考え方がたくさんあるのです。
今回は知能テストの理論を大学入試のセンター試験に当てはめて考えてみたいと思います。
「良いテスト」とは一体どんなものでしょうか?

測りたい能力を数値化できているか
そもそも、なぜ大学に入学するのに学力が要求されるのでしょうか?
一部のAO入試のように例外はあるものの、今も入試の多数派は学力試験が占めています。
公平な選抜であれば良いというだけなら、筋力やくじ引きで選んでもいいんじゃないでしょうか?
これは「大学入試」という存在を自明視する立場からは答えにくい質問かもしれません。
結論から言えば、
「それが大学入学後の成績と相関するから」
という功利主義的な解答が最もシンプルでしょう。※1
大学に一度入学させた学生が、最後まで卒業出来なかったり、周囲の学生の足を引っ張るようなことがあると、大学にとって不利益となります。
(さらに、「入学した大学の学力が合わない」ことは学生自身にとっても不利益となりえますが、
これについては愚行権の観点からグレーな問題なので保留させていただきます)
逆に、優秀な知的パフォーマンスを持つ学生が入学すれば、勉学の面で周囲の学生にポジティブな効果を与えることが期待されますし、「その大学から優秀な人材が卒業する」という形で大学のブランドを更に向上させることにも繋がります。
私立の大学であれば、このように実利の観点から「学力で選抜する」ことを正当化しえます。
国立大学ではもう一段階の議論の余地はあるものの、「限られた教育リソースを、公平かつ効率的に、客観的に正当化しうる方法で希望者に分配する」という観点からは、先述の功利主義的な議論を敷衍できるかと思います。
これ以上掘り下げると議題が心理学の範疇を超えるので、記事内ではこの話題はここまでにします。
(社会科学や政治哲学の観点からここを詰めてくださる方がいましたら歓迎致します)
さて、この流れに沿って「大学入試が学力による選抜を採用する意義」をまとめるならば、
「高校の勉強の学力が高いほど、大学での学力到達度が高いと予測される」から
「大学入学の優先権が与えられるのは妥当である」という話になるでしょう。
これは例えば、「入試で問うべき英語力とは何であるか」という問いに示唆を与えます。
多くの学部では、論文を英語で読み書きすることになります。
つまるところ、大学入試では「『学問で必要となる英語の能力』が高いと予測される人を選ぶ試験」こそが「良い試験」であると言えるのではないでしょうか。
「実用的な英語力」などという漠然としたお題目では、「実用的な英語力を測れているのか」という問いを立てると同時に「実用的な英語力とは何か」という二重の問題が発生してしまいます。
何よりもまず「何のために英語の能力で大学入学者を選抜するのか」という具体的なコンセプトの再確認が大事ではないでしょうか。
※1 「センター試験の成績が良いほど大学での成績が良い」という明らかな一貫した傾向を統計で示すのは現状の日本の進学環境では難しいです。何故ならば、センター試験で高得点の者ほど上位の大学に進学する傾向があり、その大学内では同ランクの者同士が相対評価で優劣を付けられるからです。
しかし間接的な証拠として、「大学の入学ボーダーを下げた結果、学生の平均レベルが低下した」といった現象は指摘されています。これは「大学入試時点での成績が高いほど大学での学業成績が良い」という傾向の傍証と考えられるのではないでしょうか。
能力の高低が点数の高低と安定して一致するか
前項では試験の「質」≒「内容」について触れました。
では、「量」≒「難度」はどうでしょう。
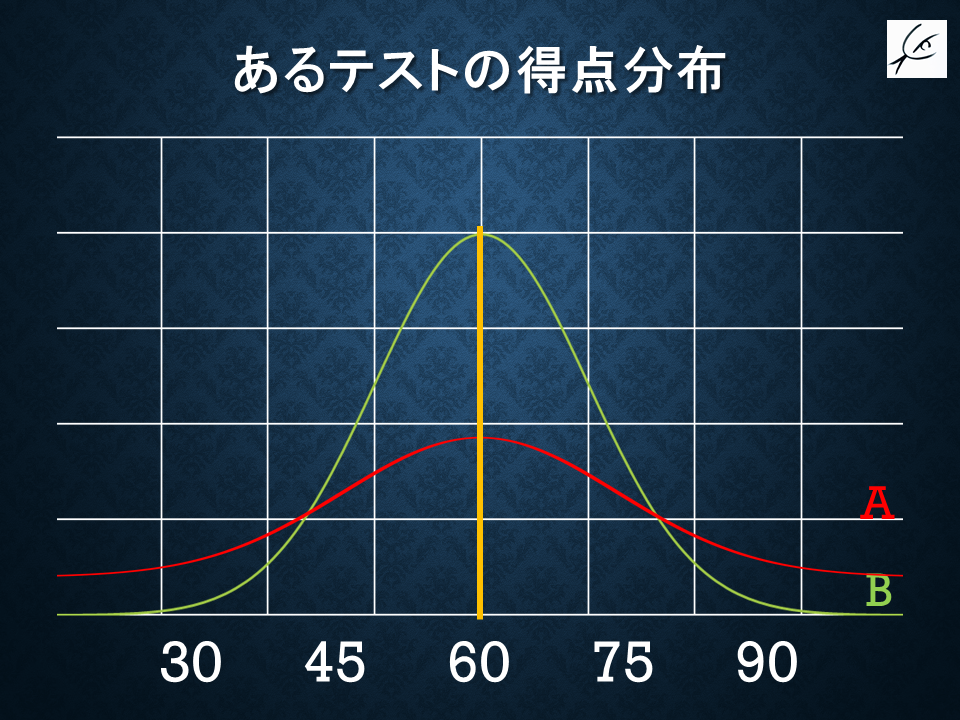
ある試験AとBの結果を、「得点」を横軸、「人数」を縦軸として、
「どの得点帯にどれくらいの人がいるか」で図示したとしましょう。
同じ平均点だとしても、このように異なる分布がありえます。
ここで、「あらゆる実測値には誤差がある」という統計の大前提を知っておいて下さい。
この「誤差」に「受験者と出題との相性によるムラ」までを含めるかどうかは微妙なところですが、出題以外にも様々な要因で「一貫性のない点数変動(≒誤差)」は発生しえます。
例えば、受験者の問題文の見まちがいや、当日のコンディション、あるいは採点者によるブレや集計ミスなどなど……
こうした学力とあまり関係のない誤差は、難度によらず一定の幅で発生しうるはずです。
ここで便宜的に、「合格ボーダーが60点」で「誤差幅は一律に±5点」だと仮定しましょう。
「真に学力が高い人をなるべく多く合格させ、真に学力が低い人をなるべく多く不合格にする」ことを目的とした場合、先ほどのグラフではどちらの方が統計的に優れた試験でしょう?
結論から言えば、これは赤の「グラフA」ということになります。
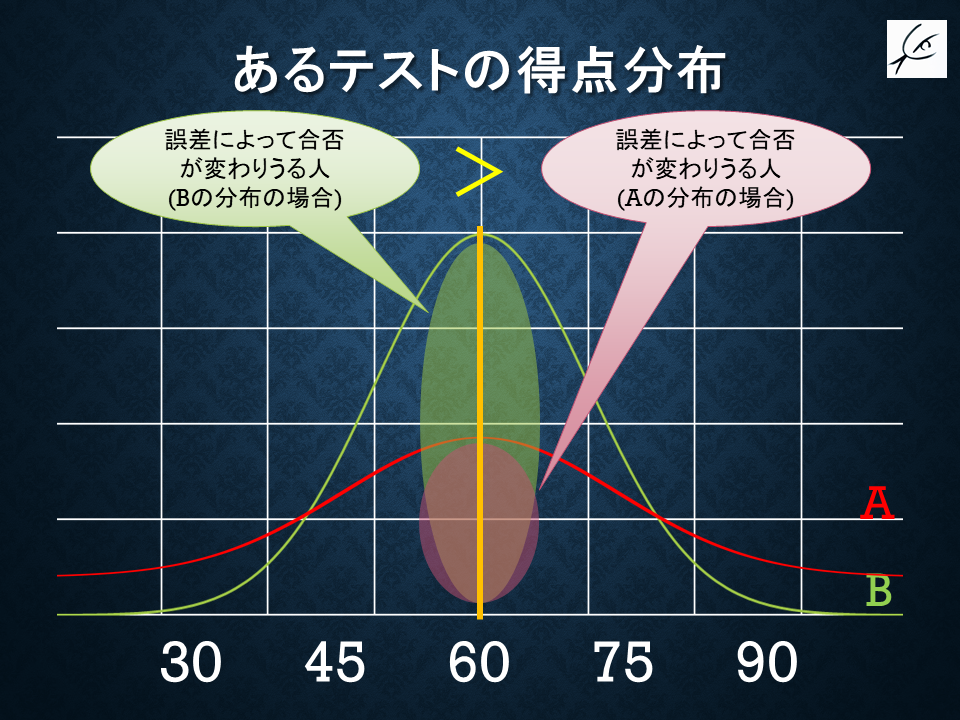
誤差幅が一律であると仮定すると、ボーダーライン付近に高い密度で受験者が集中しているほど、「誤差」の影響が大きくなってしてしまいます。
「本当は実力がないのにちょっと点が高くなって合格する人」や「本当は実力があるのにちょっと点が低くなって不合格になってしまう人」が多くなるのが、Bのグラフなのです。
もうちょっと一般化して言えば、
「区別したい学力層の人たちがあまり密集せず、上と下に広く分布するようになる」
のが、解像度の高い「良い試験」ということになります。
ちなみに、分布を変えないで「テストの解像度を下げる」方法があります。
実は「テストの解像度を下げる」簡単な方法はですね……
「1点刻みのテストを10点刻みにする」のです。

これによって、「本当は弁別されるべき53点と50点の人」が「同じ50点」になったり、「本当は僅差であるはずの54点と55点の人」が「10点差の50点と60点」になったりします。

これほどお手軽に「試験の性能を下げる」方法はなかなか他にありませんよね。
え?そんなの嬉しくないから誰も使わないって?
まぁそうですよね。普通に考えたら当たり前です。
さて、得点中間層の話と別に、上位層と下位層では異種の問題が出じます。
「天井効果」と「床効果」と言われるものです。
小学校のテストのクラス内順位が「100点10人で同点1位」みたいになった経験はありませんか?
受験者に対して問題が簡単すぎると、得点の上限付近の解像度が悪くなります。
上の例で言えば、「11位以降」は95点や80点で比較出来るのに対し、「学力が1位の人と10位の人」は同点になってしまうので、このテストで区別することが出来ません。
これを「天井効果ceiling effect」と言います。
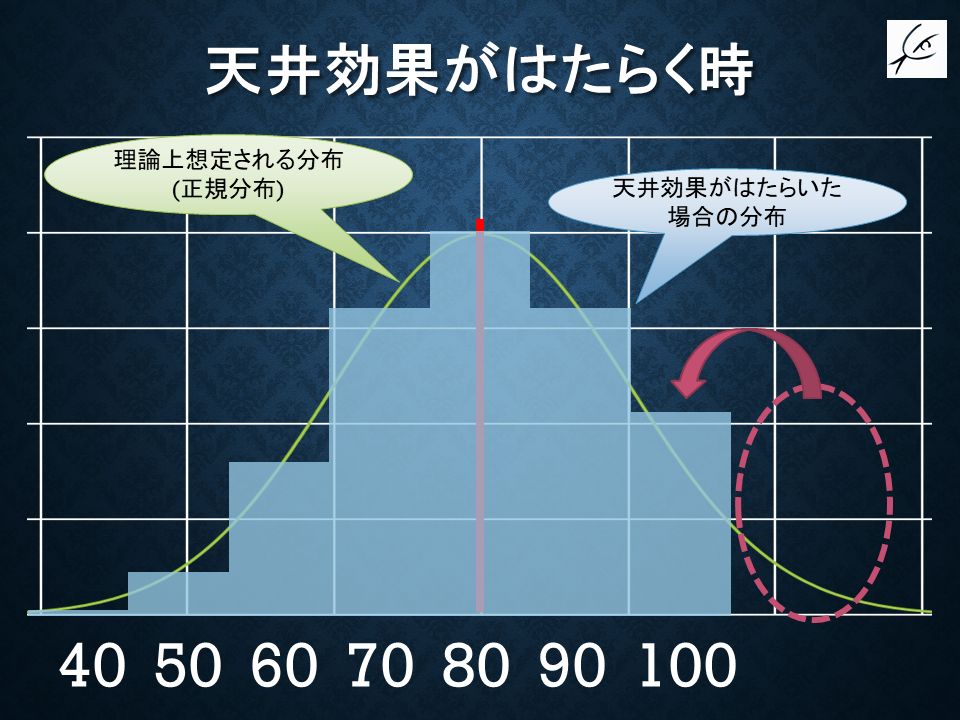
難関大学はセンター試験レベルでは多くの科目で天井効果が出てしまいますが、二次試験があるため、結果的に受験者を適切に弁別できるようになっているのです。
逆のパターンを考えてみましょう。
クラスの過半数が0点を取るような難しすぎるテストでは、下位層は一塊になってしまいます。
これを「床効果floor effect」と言います。

「大量の0点」は記述式でなければなかなか起こりえませんが、選択式でも実質的にそれと近いことは起こります。
4択式の選択問題で0~30点付近(つまり期待値程度の得点帯)の場合、真の学力に比べて誤差が十分に大きくなってしまうので、これも一種の床効果とみなせるでしょう。
例えば、TOEFL iBTのような難度の高い試験を平均ちょい下くらいの高校で全員に受験させたら、これもやはり床効果がそれなりに出るのではないかと思います。
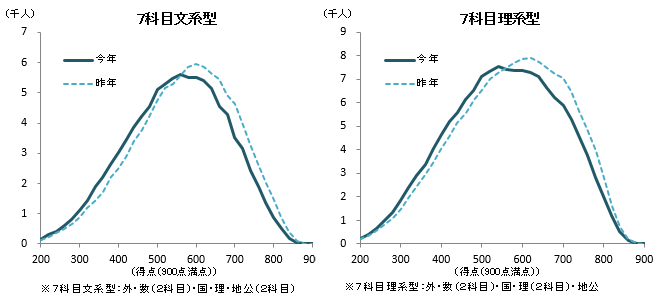
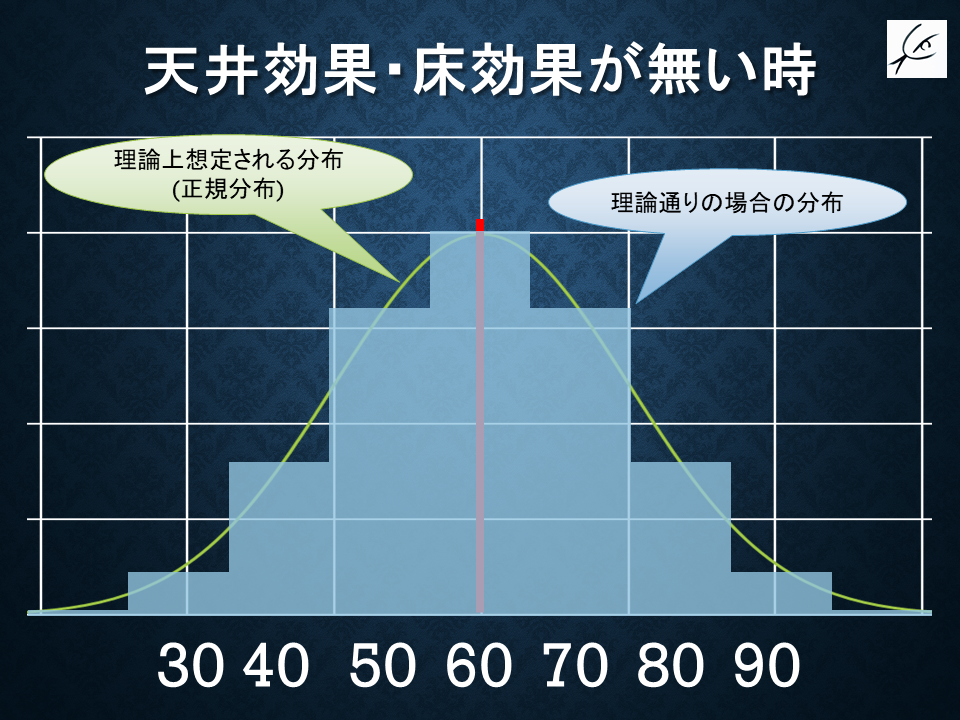
では、現状のセンター試験の分布を見てみましょう。
総合得点の分布を見ると、これは全国統一のテストとしては非常によく分散していると思えます。
中間にピークがありつつも最頻値付近に極端に密集しているわけでもなく、どの得点帯でも解像度が保たれているように思えます。
また、上位層も下位層もなだらかに減衰しており、天井効果・床効果はあまり出ていないことが見て取れます。
「これからはもっと高い学力が必要だから」と言って難易度を無闇に上げるのは、実は「テストの弁別性能」という発想からは肯定しにくいものです。
「平均学力を上げるための介入」をせずに問題の難度だけ上げると、下位層で床効果が優勢になってしまうからです。
「床効果」が出てしまうというのはつまり、「苦手な科目はちょっとくらい勉強しても勉強しないのと同じ」になってしまうということです。
上位の大学には二次試験があることを考えると、センター試験で特に問題視すべきは、天井効果よりも床効果であるはずです。
センター試験の難度を無闇に上げることは、「テストの解像度が下がる」危険性を孕んでいると言えるでしょう。
社会的合意が得られる方法であるか
2001年にカリフォルニア大学の学長が、SAT-Iの「abstract reasoning tests」のようなテストを強く批判し、SAT-Iを入試に採用することを中止する声明を出しました。
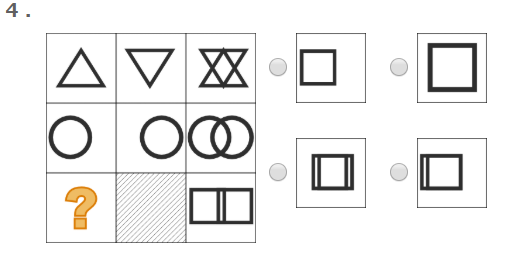
この「abstract reasoning tests」というのは、こんな感じのやつです。
ピンときた方も多いんじゃないでしょうか。
ネットでいわゆる「IQテスト」として出てくる問題の定番ですよね。
WAISには「行列推理」という名前でこれと近いテストが入っています。
実際の(いわゆる)「知能テスト」でも類似の形式の問題は採用されているわけですし、このテストは一般知能との相関が高いことも実証されています。
統計的に言えば、「一見意味が無さそうでも、学力と統計的に相関があれば正当化しうる」はずでしょう。
しかし批判の中核は、これが「知的能力を弁別する機能がない」という話ではありませんでした。
知能テストが入試に使われることの何が問題なのか?
これを理解するには、「abstract reasoning tests」が「富裕層だけが有利に対策できるテストである」という背景を知るべきでしょう。
この背景を知らない日本では、「知能テストに採用されている」というと、無条件に
「ジアタマの良し悪しを見るテスト」だと思ってしまう人が多いかもしれません。
実はそんなことは全くありません。
この推論テストにも実はパターンがあり、対策が通用してしまいます。
だからこそ、専用の対策を教える塾や教材がアメリカでは商売として成立しています。
しかも、通常の理科や社会のような学科試験と異なり、こんな問題は普通に学校のクラスで勉強しても習うことはありません。
「入試以外の場面ではまずお目にかからない」ということは、「入試のためだけの対策に金を払える人」が極端に有利になってしまう方式と考えられるのです。
その上、ここで培われたノウハウは全く学問的な知識やスキルではないので、この対策に費やされる労力はホトンドが「入試で人より優位に立つため」だけに浪費されます
――つまり社会的な損失でしかないのです。
この問題は追求しすぎるときりがないので、端的にまとめます。
「社会的観点から入試に求められる公正さ」として、以下の二点が最低限の入試のモラルとして要求されることを指摘しておきます。
・そのテストの対策法が一部の業者や階層に独占されていないこと
・そこで要求される能力が少なくとも大学での学問や教養の基礎となること
この2点が損なわれれば、「一部の特権階層に有利な選抜」や「選抜で勝つためだけにコストを支払えるかどうかの競争」になってしまいます。
一点目の問題は「仕組み」によってある程度防ぐことが出来ますが、二点目の問題を回避するには「そのテストでだけ通用するローカルな裏技」が存在しないようにする必要があるので、当然ながら作問者の深い学識とそれなりの作問コストがかかります。
さて、「民間の業者とは独立の製作委員会がコストをかけて作るテスト」と、「民間の業者が採算を取るために低コストで作るテスト」では、どちらの方がこの目的を達成しやすいでしょうか。
入試は「大学で必要とされる能力の基礎」を問うからこそ一種の差別が許容されているのであり、
「大学と学生の将来の利益」に繋がる形で妥当性と有用性を担保しなければ正当化はできません。
また、「国立大学で学ぶ者を選抜する」という目的から、そのあり方は「公正で中立な競争」でなければ社会的疑義が生じるでしょう。
以上、心理検査と統計の観点から大学入試の「良い試験/悪い試験」について考えてみました。
今回の記事はここまでにします。
なお今回の記事に関しては、内容の一切は筆者・木村の個人の思考と所感に基づくものであることを申し添えておきます。
おわりに
★ひとことまとめ
3. その能力競争が「社会的に見て公正なものかどうか」も大事
★参考文献
・書籍
1.Earl Hunt: Human Intelligence(2010, Cambridge University Press)
・動画
南風原朝和:
心理統計学の基礎 ―統合的理解のために.
有斐閣アルマ, 2002/6/1
人文系学生の統計学書としては定番中の定番。
以前の記事でも統計の教科書は多少紹介しましたが、こっちはかなりガチな人向け。
タイトルで「文系向け」とあなどるなかれ。
この一冊をちゃんと理解できたら、世の中の「統計学入門書」はほぼ不要になるくらいです。
★この研究会について
以下の書籍の輪読会をインターネット上にて定期開催しています。
Earl Hunt: Human Intelligence(2010, Cambridge University Press)
本記事は輪読会の内容を元に、メンバーのトークも盛り込んでサマライズしたものです。
トピックや話の流れは上記のテキストを踏襲していますが、内容は再解釈の上で大幅に加筆や再編を加えています。
なお、研究会に参加をご希望の方はこちらの記事をご覧ください。
この記事を書いた人
狐太郎
最新記事 by 狐太郎 (全て見る)
- AIサービスを活用した英文メール高速作成術 - 2023年3月28日
- 大学生・院生に便利なAIウェブサービスまとめ【2023年2月版】 - 2023年2月22日
- 「読書強者」が「速読」に価値を見出さない理由【隙間リサーチ】 - 2022年9月23日