前川 淳:
本格折り紙―入門から上級まで.
日貿出版社, 2007/7/1
BACKGROUND ――対象
「普段は科学系の本を中心に紹介しているのに、今回は急に子供向け?」
いえいえ、そんな事はありません。
確かにこれは折り紙の本ですし、子どもでも作れるような作品も紹介されています。
しかし、本書の真骨頂は「数学の分かる大人」にこそ面白く感じられるはずです。
本書の著者の本業はソフトウェアエンジニア。そう、ガチガチの理系です。
しかし筆者の言を借りれば、折り紙は「文系と理系とアートが地続きになった」ものだとか。
そしてまた著者によれば、「折り紙らしさ」とは「幾何学と造形が調和した、発見の感じられる紙によるデザイン」であるというのです。
そんな折り紙の真髄が詰まった一冊が本書。
「綾辻行人が絶賛した折り紙の本」
「日経サイエンスに掲載された折り紙作品」
どんなものだか、気になってきませんか?
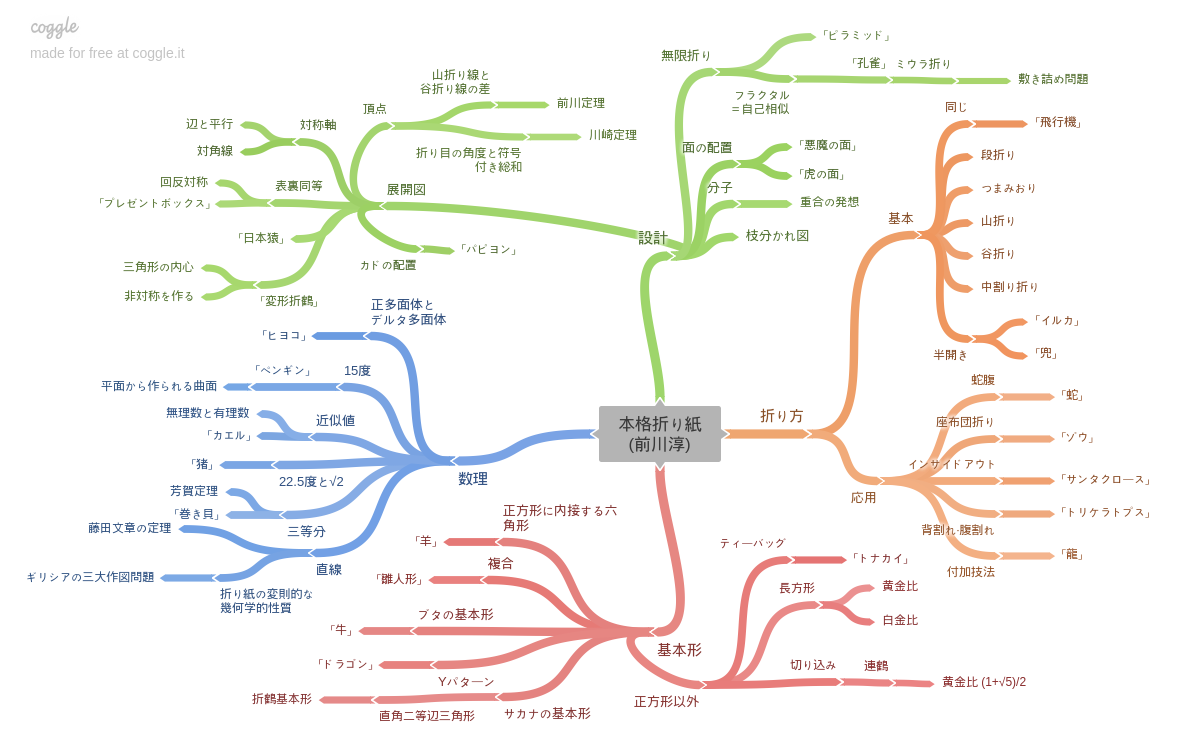
METHODS ――目次
RESULTS ――所感
図だけ見ながら作ってみると、一見普通の「折り紙作品集」のようにも見えます。
(それでも変わった作品がちらほらありますが)
しかし、本書がすごいのは、その充実した解説文章。
著者自身も「解説の多い本です。いわば、作品の紹介を通した、折り紙の教科書です」と述べているように、折り紙や幾何学に関する理論が惜しみなく散りばめられています。
図の掲載と同じくらい文章書いてるんじゃないのか、というくらい。
立体的な造形を、平坦でない多面体として実現することを考えた場合、重要となるのは、外側に現れる面をどのように配置するかです。
-P.94
角を規格化する場合、その最小単位は15度と22.5度が扱いやすく、30度がそれに準じ、18度などはかなり手強いというのが実感です。なお、15度を単位にした場合、面として現れる三角形は、22.5度を単位にした場合の5種に比べて、12種と、ぐっと増えます。
-P.98
表裏同等折りは、川崎敏和さんが、「表裏同等立方体」などの作例とともに提唱した概念で、結晶学などでいう「回反対称」に相当します。
-P.61
……こんな解説文に「折り紙の本」でお目にかかったことがあるでしょうか。
私は全く初めてで、非常に衝撃を受けました。
作品自体は子どもでも作れそうなものが半分くらいはありますが、明らかに主として意識されている対象層は大人です。それも、数理と芸術の融合が大好きな大人。
幾何学として面白いのは勿論のこと、「折り紙で自分のオリジナル作品をデザインしたい」と思う人にとっても、本書は最適解だと思います。
本書の解説文は、難しければ読み飛ばしても作品は作れるようになっていますし、逆に解説で幾何学のエッセンスだけ味わって作品は作ったつもりで読み進めることもできます。
しかし、やはり「相乗効果」こそが本書の白眉。
解説を読んで、「こんな幾何学的な法則が潜んでいたのか」と思いながら作ることで、実際にその操作の数学的意義を意識しながら作品が作れる。
そんな風に一つ一つの作品が「テーマ」を持って配置されています。
もちろん作品としても優れていて、非常に見栄えの良い作品が無理なく折れました。
CONCLUSIONS ――結語
「大人になってまで折り紙なんて……」という逡巡を一瞬で吹き飛ばしてくれる面白さ。
「自分の手で実感できる幾何学」という点で、折り紙は素晴らしい知的遊戯ですね。
「子供の頃の素朴な遊び」が「奥深い幾何学の世界」に変貌する興奮は格別でした。
こんな人にオススメ
★小さい頃に折り紙にハマった人
★空間や図形を扱うのが好きな人
★数学IAの問題が好きだった人
前川 淳:
本格折り紙―入門から上級まで.
日貿出版社, 2007/7/1
狐太郎
最新記事 by 狐太郎 (全て見る)
- AIサービスを活用した英文メール高速作成術 - 2023年3月28日
- 大学生・院生に便利なAIウェブサービスまとめ【2023年2月版】 - 2023年2月22日
- 「読書強者」が「速読」に価値を見出さない理由【隙間リサーチ】 - 2022年9月23日